スミス(Smith)分解を使って,格子を解析する
ベクトル 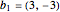 と
と 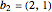 の倍数である整数によって生成された格子
の倍数である整数によって生成された格子 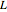 を考える.
を考える.
In[1]:=
b1 = {3, -3};
b2 = {2, 1};In[2]:=
ptsb = Flatten[Table[j b1 + k b2, {j, -12, 12}, {k, -12, 12}], 1];In[3]:=
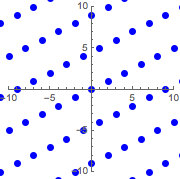
graphicsb =
Graphics[{Blue, PointSize[Large], Point@ptsb}, PlotRange -> 10,
Axes -> True]Out[3]=
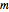 を,行が
を,行が 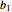 と
と 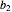 の行列とする.
の行列とする.
In[4]:=
m = {b1, b2};スミス分解は恒等式 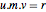 を満足する3つの行列を与える.
を満足する3つの行列を与える.
In[5]:=
{u, r, v} = SmithDecomposition[m];In[6]:=
u.m.v == rOut[6]=
行列 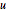 と
と 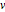 は整数の要素と行列式1を持つ.
は整数の要素と行列式1を持つ.
In[7]:=
{u // MatrixForm, v // MatrixForm, Det[u], Det[v]}Out[7]=
行列 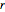 は整数であり対角行列である.その項目から,
は整数であり対角行列である.その項目から,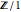 は自明群なので,群
は自明群なので,群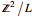 の構造は
の構造は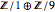 (単純に
(単純に 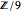 )であることが分かる.
)であることが分かる.
In[8]:=
r // MatrixFormOut[8]//MatrixForm=
恒等式 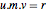 に
に 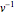 を掛けると
を掛けると 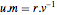 になる.
になる.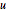 は整数であり,行列式は
は整数であり,行列式は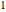 なので,
なので,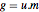 は
は 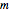 と等しいが格段に単純な格子を生成する.
と等しいが格段に単純な格子を生成する.
In[9]:=
g = r.Inverse[v];
g // MatrixFormOut[9]//MatrixForm=
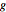 の行によって生成された格子を可視化する.
の行によって生成された格子を可視化する.
In[10]:=
ptsg = Flatten[
Table[j First[g] + k Last[g], {j, -12, 12}, {k, -12, 12}], 1];In[11]:=
graphicsg =
Graphics[{Red, PointSize[Medium], Point@ptsg}, PlotRange -> 10,
Axes -> True]Out[11]=
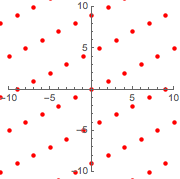
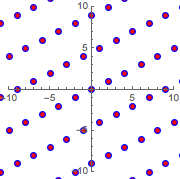
新しい格子をもとの格子に重ねると,両方同じであることが確認できる.
In[12]:=
Show[{graphicsb, graphicsg}]Out[12]=