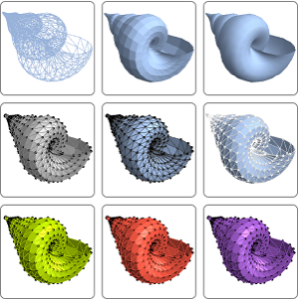
Euler Rotations

Version 11 introduces EulerMatrix to describe a sequence of rotations with respect to a moving coordinate frame.

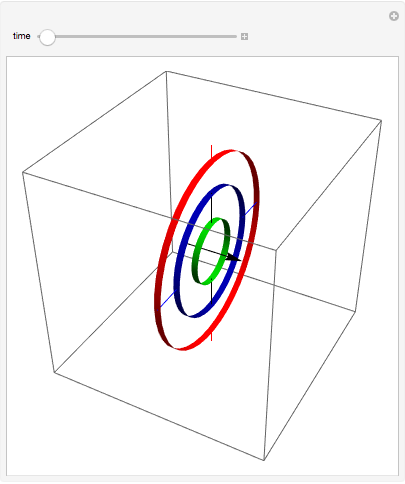
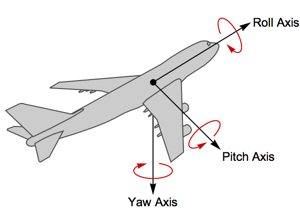
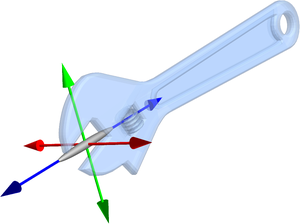
Model a gimbal. Each Euler angle is the relative angle of turn for each axis.

In[1]:=

ring3 = {Red, CapForm -> None, Tube[{{-.1, 0, 0}, {.1, 0, 0}}, 3], Line[{{{0, 0, 4}, {0, 0, 3}}, -{{0, 0, 4}, {0, 0, 3}}}]}; ring2 = {Blue, CapForm -> None, Tube[{{-.1, 0, 0}, {.1, 0, 0}}, 2], Line[{{{0, 3, 0}, {0, 2, 0}}, -{{0, 3, 0}, {0, 2, 0}}}]}; ring1 = {Green, CapForm -> None, Tube[{{-.1, 0, 0}, {.1, 0, 0}}, 1], Black, Arrow[{{-1, 0, 0}, {1, 0, 0}}], Line[{{{0, 0, 1}, {0, 0, 2}}, -{{0, 0, 1}, {0, 0, 2}}}]};

In[2]:=

gimbal[{\[Alpha]_, \[Beta]_, \[Gamma]_}] := Graphics3D[{GeometricTransformation[ring3, EulerMatrix[{\[Alpha], 0, 0}]], GeometricTransformation[ring2, EulerMatrix[{\[Alpha], \[Beta], 0}]], GeometricTransformation[ring1, EulerMatrix[{\[Alpha], \[Beta], \[Gamma]}]]}, ViewPoint -> {1.3, -2.4, 2.}, PlotRange -> 3.5, ImageSize -> Medium];

In[3]:=

gimbalframes = Table[gimbal[{i, i, i}], {i, 0, 2 Pi, Pi/32}];

In[4]:=

Manipulate[ gimbalframes[[i]], {{i, 1, "time"}, 1, Length[gimbalframes], 1}, SaveDefinitions -> True]

Out[4]=

Play Animation

Stop Animation