Mesh from Arrays: New in Wolfram Language 11

Mesh from Arrays

Generating color tetrominoes and building chessboards or arbitrary geometric shapes from patterns is easy in Version 11.

In[1]:=

arrays = {\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "0", "0", "0"},
{"1", "0", "0", "0"},
{"1", "0", "0", "0"},
{"1", "0", "0", "0"}
},
GridBoxAlignment->{
         "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, 
          "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, 
          "ItemsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]}, 
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, 
          "ItemsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$, 
MatrixForm[BoxForm`e$]]]\), \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "1", "0", "0"},
{"0", "1", "0", "0"},
{"0", "1", "0", "0"},
{"0", "0", "0", "0"}
},
GridBoxAlignment->{
         "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, 
          "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, 
          "ItemsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]}, 
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, 
          "ItemsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$, 
MatrixForm[BoxForm`e$]]]\), \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "1", "0", "0"},
{"1", "0", "0", "0"},
{"1", "0", "0", "0"},
{"0", "0", "0", "0"}
},
GridBoxAlignment->{
         "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, 
          "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, 
          "ItemsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]}, 
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, 
          "ItemsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$, 
MatrixForm[BoxForm`e$]]]\), \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"0", "1", "0", "0"},
{"1", "1", "0", "0"},
{"0", "1", "0", "0"},
{"0", "0", "0", "0"}
},
GridBoxAlignment->{
         "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, 
          "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, 
          "ItemsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]}, 
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, 
          "ItemsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$, 
MatrixForm[BoxForm`e$]]]\),
   \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "0", "0", "0"},
{"1", "1", "0", "0"},
{"0", "1", "0", "0"},
{"0", "0", "0", "0"}
},
GridBoxAlignment->{
         "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, 
          "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, 
          "ItemsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]}, 
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, 
          "ItemsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$, 
MatrixForm[BoxForm`e$]]]\), \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "1", "0", "0"},
{"1", "1", "0", "0"},
{"0", "0", "0", "0"},
{"0", "0", "0", "0"}
},
GridBoxAlignment->{
         "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, 
          "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, 
          "ItemsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]}, 
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, 
          "ItemsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$, 
MatrixForm[BoxForm`e$]]]\), \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "1", "0", "0"},
{"0", "1", "1", "0"},
{"0", "0", "0", "0"},
{"0", "0", "0", "0"}
},
GridBoxAlignment->{
         "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, 
          "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, 
          "ItemsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]}, 
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, 
          "ItemsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$, 
MatrixForm[BoxForm`e$]]]\)};

In[2]:=

col = ColorData[97, "ColorList"];

In[3]:=

Table[ArrayMesh[arrays[[i]], MeshCellStyle -> {2 -> col[[i]]}], {i, 
  7}]

Out[3]=

Build a 3D chessboard.

In[4]:=

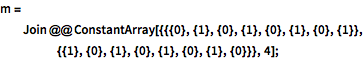
m = Join @@ 
   ConstantArray[{{{0}, {1}, {0}, {1}, {0}, {1}, {0}, {1}}, {{1}, \
{0}, {1}, {0}, {1}, {0}, {1}, {0}}}, 4];

In[5]:=

p = First /@ Position[Flatten[m], 1];

In[6]:=

style = {{1, All} -> {Thick, Black}, {3, All} -> 
    White, {3, #} & /@ p -> Black};

In[7]:=

r = ArrayMesh[ConstantArray[1, {8, 8, 1}], MeshCellStyle -> style]

Out[7]=

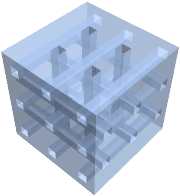
Construct a Seidel mesh, a region with tunnels going in every direction without crossing.

show complete Wolfram Language input

In[8]:=

seidelArray[{r_, s_, t_}] := 
 Table[If[Mod[i, 4] == 2 && Mod[j, 4] == 2 || 
    Mod[i, 4] == 0 && Mod[k, 4] == 0 || 
    Mod[j, 4] == 0 && Mod[k, 4] == 2, 0, 1], {i, 3 + r 4}, {j, 
   3 + s 4}, {k, 3 + t 4}]
transparentMesh[mr_?MeshRegionQ] := 
 HighlightMesh[
  BoundaryMesh[mr], {Style[1, None], Style[2, Opacity[0.5]]}]

In[9]:=

transparentMesh[ArrayMesh[seidelArray[{2, 2, 2}]]]

Out[9]=

Implement Conway's Game of Life.

In[10]:=

gameOfLife = {224, {2, {{2, 2, 2}, {2, 1, 2}, {2, 2, 2}}}, {1, 1}};
board = RandomInteger[1, {40, 40}];

In[11]:=

sim = NestList[Last[CellularAutomaton[gameOfLife, #, {{0, 1}}]] &, 
   board, 70];

In[12]:=

ListAnimate[ArrayMesh /@ sim]

Out[12]=

Play Animation

Stop Animation

Wolfram Language™

Mesh from Arrays

Related Examples