Symbolic PDEs over Regions

Version 11 adds extensive support for symbolic and numerical solutions of boundary value problems over regions.

Dirichlet problem for the Laplace equation in a disk.

In[1]:=

leqn = Laplacian[u[x, y],{x, y}] == 0;

In[2]:=

dcond = DirichletCondition[u[x, y] == Sin[6 ArcTan[y/x]], True];

In[3]:=

\[CapitalOmega] = Disk[{0, 0}, 3];

Symbolically solve on the unit disk with Dirichlet boundary condition.

In[4]:=

sol = DSolveValue[{leqn, dcond}, u[x, y], {x, y} \[Element] \[CapitalOmega]]

Out[4]=

In[5]:=

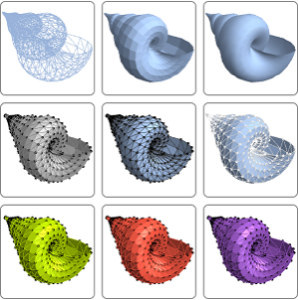
Plot3D[sol, {x, y} \[Element] \[CapitalOmega], PlotRange -> All, PlotStyle -> Hue[0.5], Exclusions -> None]

Out[5]=