Substitution Systems

SubstitutionSystem generates a list representing the evolution of a given initial state following the iterative applications of a set of rules.

Consider the following initial state and set of rules.

In[1]:=

init = "\[Wolf]"; rules = {"\[HappySmiley]" -> "\[Wolf]\[HappySmiley]", "\[Wolf]" -> "\[HappySmiley]"};

Use SubstitutionSystem to get its evolution over 8 iterations.

In[2]:=

SubstitutionSystem[{"\[HappySmiley]" -> "\[Wolf]\[HappySmiley]", "\[Wolf]" -> "\[HappySmiley]"}, "\[Wolf]", 8] // Column

Out[2]=

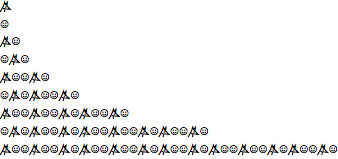
Use a two-dimensional set of rules to construct the Sierpiński carpet.

In[3]:=

rules2D = {1 -> {{1, 1, 1}, {1, 0, 1}, {1, 1, 1}}, 0 -> ConstantArray[0, {3, 3}]};

Visualize this substitution system using RulePlot.

In[4]:=

RulePlot@SubstitutionSystem[rules2D]

Out[4]=

Generate the Sierpiński carpet.

In[5]:=

ArrayPlot /@ SubstitutionSystem[rules2D, {{1}}, 5]

Out[5]=