A Submarine Cable

Compute the geodesic length of a submarine communication cable under the Pacific Ocean.

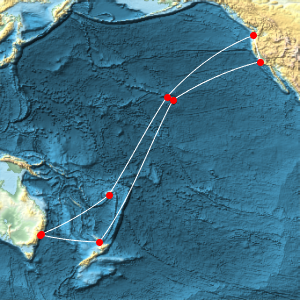
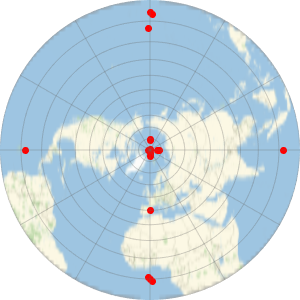
This GeoPosition object contains 9 landing points for the Southern Cross Cable.

In[1]:=

landings = GeoPosition[{{-33.913939, 151.196199}, {-33.761205, 151.273933}, {-18.12381, 178.437397}, {21.354003, 201.869442}, { 45.824792, 236.188811}, {35.366692, 239.152774}, {20.023145, 204.177937}, {-36.787961, 174.767867}, {-36.78884, 174.623336}}];

Represent the cable as a GeoPath object joining consecutive landing points with geodesic segments. The actual physical cable does not follow exact geodesics, so this is a minimizing approximation. This cable has closed topology.

In[2]:=

cable = GeoPath[landings, CurveClosed -> True];

Draw the cable and its landing points over a relief equirectangular map of the Pacific Ocean.

In[3]:=

GeoGraphics[{White, cable, Red, PointSize[Large], Point[landings]}, GeoRange -> Entity["Ocean", "PacificOcean"], GeoBackground -> "ReliefMap"]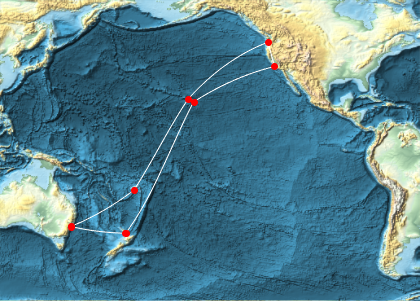

Out[3]=

Compute the total length of the geodesic approximation to the cable.

In[4]:=

GeoLength[cable, UnitSystem -> "Metric"]

Out[4]=

The Wikipedia article quotes 28,900 km of submarine and 1,600 km of terrestrial cable, hence a total of 30,500 km. Therefore, the cable is about 4,000 km longer than the minimal curve joining the landing points with geodesics.

In[5]:=

GeoLength[cable, UnitSystem -> "Metric"]; Quantity[30500, "Kilometers"] - %

Out[5]=