Travel Time & Distance
Estimate distance and duration of a road trip.
Travel between two distant cities.
In[1]:=
cities = {Entity["City", {"Lisbon", "Lisboa", "Portugal"}],
Entity["City", {"Beijing", "Beijing", "China"}]};This is the geodesic distance between them.
In[2]:=
GeoDistance[cities]Out[2]=
This is the length of the computed road trip.
In[3]:=
TravelDistance[cities]Out[3]=
And this is the estimated driving time, assuming continuous driving with no stops.
In[4]:=
TravelTime[cities]Out[4]=
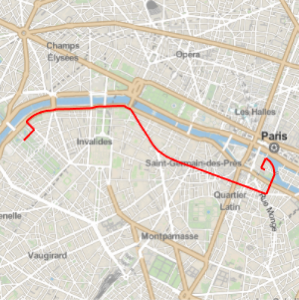
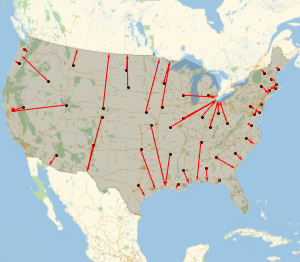
This object contains the actual set of travel instructions.
In[5]:=
td = TravelDirections[{Entity[
"City", {"Lisbon", "Lisboa", "Portugal"}],
Entity["City", {"Beijing", "Beijing", "China"}]}]Out[5]=
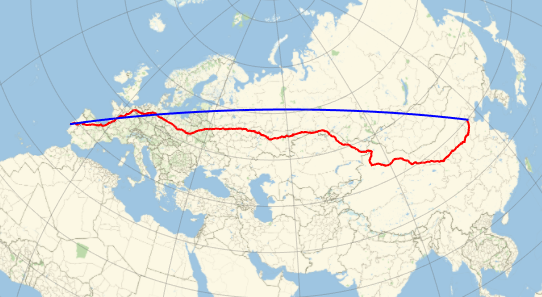
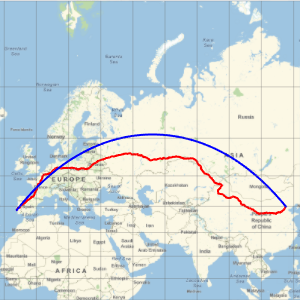
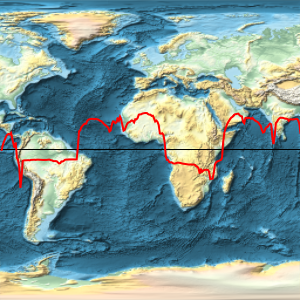
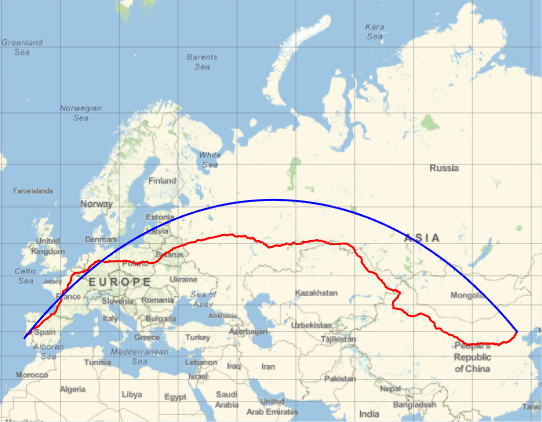
Represent the trajectory (in red) on a Mercator map and compare with the geodesic trajectory (in blue), which is shorter, as you saw before.
In[6]:=

GeoGraphics[{Thick, Red, GeoPath[td], Blue,
GeoPath[{Entity["City", {"Lisbon", "Lisboa", "Portugal"}],
Entity["City", {"Beijing", "Beijing", "China"}]}]},
GeoProjection -> "Mercator", GeoGridLines -> Automatic]Out[6]=
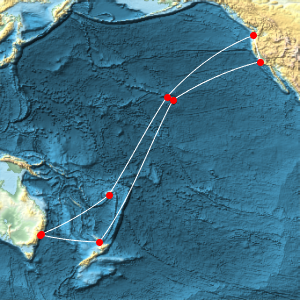
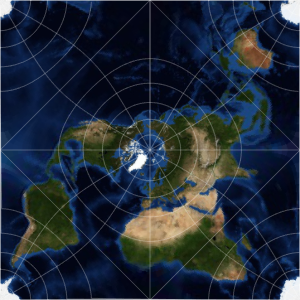
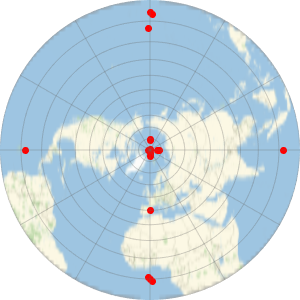
An azimuthal projection shows more clearly that the geodesic is shorter than the travel path.
In[7]:=
GeoGraphics[{Thick, Red, GeoPath[td], Blue,
GeoPath[{Entity["City", {"Lisbon", "Lisboa", "Portugal"}],
Entity["City", {"Beijing", "Beijing", "China"}]}]},
GeoProjection -> "Mercator", GeoGridLines -> Automatic];
Show[%, GeoProjection -> "LambertAzimuthal", GeoZoomLevel -> 4]Out[7]=