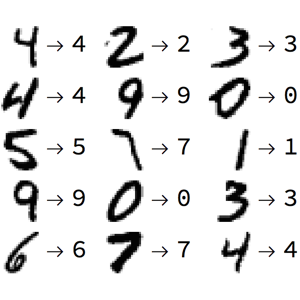Object Classification
Using the CIFAR-10 database of labeled images, train a convolutional net to predict the class of each object.
First obtain the training data.
In[1]:=

obj = ResourceObject["CIFAR-10"];
trainingData = ResourceData[obj, "TrainingData"];
RandomSample[trainingData, 5]Out[1]=
Extract the unique classes.
In[2]:=
classes = Union@Values[trainingData]Out[2]=
Create a convolutional net that predicts the class given an image.
In[3]:=

lenet = NetChain[
{ConvolutionLayer[20, 5], Ramp, PoolingLayer[2, 2],
ConvolutionLayer[50, 5], Ramp, PoolingLayer[2, 2], FlattenLayer[],
500, Ramp, 10, SoftmaxLayer[]},
"Output" -> NetDecoder[{"Class", classes}],
"Input" -> NetEncoder[{"Image", {32, 32}}]
]Out[3]=

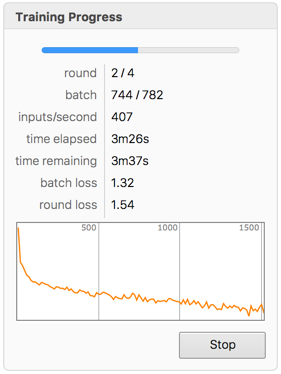
Train the net on the training data.
In[4]:=
trained = NetTrain[lenet, trainingData, MaxTrainingRounds -> 4]Out[5]=
Predict the most likely classes for a set of images.
In[6]:=
trained[{\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJylkglQU1kWhruma1qrHRQhiLIIKCKyiQKKSlS2gIiEAMoi+2ID4sYiChbt
LqiIYqugKKDYYiubrIEIhMgWQkKWlxVM2EkAQUhIINtcwJpyqnqmempO/e/k
5VXd7/z3v9cg/IzXib/98MMPCStB8wpLto+PD7vorQr+HD2dEPPL6ajIQ6cT
o36JircN/xF81P/2LL53f3hDrCym1JVAjRWc1rr+rsaRHtwYtX2cQfjaRxH1
0+eH2bLRPtlY3wK/b2GcKxXwZAKelM9dGO0T8znicY6EzxYO0ma5lJle8iSz
exzCj0NdfCB61xitE/BJVW9p6FJ64wfAHyA0jZJxfFoH4H9hk2a5NPEAQzrE
ko/1ycY/Syd5oMsES++CXsnEosRjLNEgJOqnCT9Tp9mkKRYRaHJJANJd8Tvg
Q/Vly3zgf5jUAvzzgQ0GYYrTA0bM9zMkg8xF/xPchYk+6eSiFgB5nCPks4TD
kHCAKuLRRFzabB8FjJjm9Ez3koGAQ+C/p/od1FC+zOd2Yga7m0fIrWBrAnrX
BLMbpDT3mSbk0oSDDNEoa07AlEwwJZMsIKGA+XUYmhmkAb6QRwX+gWZ6e0BQ
M5+pYCEYAcxTat8zMBX0pj/hgy1Mc8iAL+IBk/TZYYZwDBKNQ3PjdNBn+PTp
IdrXAeosjzLL/cYHW5gFHeyFSwNTSDXvyIvhV9KbKpf5Q0Qsn9I6AY4Awgug
rik2eaGfPsvpGV0c2v6FQxJyqfMjDPEXtmiSLZngzI2xxSPs2SHmFI8GyIA5
xaNM91NnBugiLkRCl5IbyqGmKga2GvB5+I+AL6C2TUEdE3T8OJP49TPEp3RQ
MRVtZUUNr3IbCp5/Kv6dWFXKJTRPcyl8JoHV3jhEIUzzGHOjbNkwSzrKEk+w
RXzWzDBTNMAg15dRP36gN1ezcLW9bejl+ymgtU/QO/mMrjFWD6sL115b0kto
EbB76K2YyhfPinN/+/3B7aLzSUWXUmM9PfzhB1KDo16l3/lYlI8vK+5Bl9Db
agQsomSYNTfCAuYBn4Gt4bSil8MZJX8SQB0COn6I0knBYTBlf0B43GgvJOAx
x3rB0qqMtJT7F5MKw2Pi9znbqOvu0dh0UMcMaWl/3AkV4+X/a2xs3s2rdY+y
hpurpSN0CqaC1ljJwALz9cA84AP/XyD8NIOEeV1Q+vQJq6ONB1HARYDwHa3o
2jdPck4HBEYedHyIOn4Ipr/tJ5j1av3tK3VM/2FoDDOzM95z+cS5gouXX4QG
UbOuiTvrgHnAZ7bU9raiQfjg8vNp7V+ZRHZD3YPExMKb6YQaAP2jMPu3m8kX
z4ZHBrt7um+xOLPL4TrymPkKFXMVTbNVWmardIxX6liobjpmBX8UEvlHWFR3
ctLU/Wvsq2ep6AoIU0kH/tvr+zsx/WBKYzWvurz2xo17ISF3gkKS3D3CXQ9H
unuGuyFDXI5429ghtY3yAmOSD3sizCx3amy0VtNx0TONsoE/DQ1rTjnPSk0a
TDo9khTXG+TViXKk1lQw0JVsbB21srg1L7s561Zr+jVS+k367XTanVuEq5fq
zsYWRv3yOCg0yz840R4RtMXk6n6XNxEng4xNYw44JTi5ZaGOVkXHdp9P+Jya
yI2JgFBuJMfdXfZWBDcEK9iXWFfOwHxoz3tUEhP9ISIMHRv1KTG2J+UsMy2p
99algd9uTTzLVrzIF+bmDN+73ZWSgA4P46SkfQqLyndwIiaeYyaeYp8Mo/gf
xiHs6nftarSwwJqZEuG2nSjPN84unJMnSA1lFQ+uP3B1emXv2IDyavX2xPsh
SSFe9BMBQ+fj+DcvDd+9MpR+cSQjWXA7afxW/OyV5LnzSQMBASRHR+IBW6yZ
AXrLOvQWVbSJbpOVDWm/fR/Ksz887O4eZxcV2BtXx5YXjzI8EJnbthbZ2ryz
tUFbWmJ3WLY72EFHkYMBfpyj3t2+SFqc/8DZkMGwoxwPRCfcGmu2tdlAD6On
g9HXxZkY4Xdtpzja0lEurOO+vSGBnOgIbMjxZCdUNAJ1125fQWjwXVOTx/q6
eZu0ivS0S3UN3hsZF+zY/srGutrEAm+zi+PpxnRzwlntfL9x88t1uu82alXp
bcBuMyTstSa7ODJRSLbfUdZxP3qoPyXcnxIWSDl54iXSrSDtavOr9zk+vg/h
9llr1uWugxXBVpeuVs1X08y0MH/o45HtYF9pu4/pimixNH6vqZmhDvP/WcV9
jdpjk609Lg60I65UXyQ5AEUP9mWGB9LDghgRgcyIAFZEMOtkTMFhl6qc+8yG
pqrL1zL32j1S0y6EaZWsVa9UUStar5tjb/fp6gV8dGSbvUOVnt5bDdV8A/1j
sA27VXVMVTRDNm5u8zxC90YR/bwpQT6MED9m0DFGgA/T14OFcmJ4IaiRQcXB
gXwykfEJh6+rTt60OX21+nMNzZcwWKn6+hqdzTU7rZuOuDbs31NruLnBcFOb
7c5cC/MkV2TuxdvhDkiPdbpoF3uurzd0zLvHw6HTeW+rgy3uoG2rE7zjkAPR
5wguIuxJUCi+urq5soJMaE8xNkldsfK55trMDWo3VNfkq2uU6mpXm29tg+/G
W23H7zZvhG/PtLV5cC6BjSMU3roXarSt3gVOR7pi4fvaD1h3udh1HkFg3d0+
uLrl2dk/sXO4BkcE7rTLvnzldW5Ofy8z29/niqZmgbr6fc0N8StW3VNb+1Jf
87n2WrSpIc7UkGxv1XxoT7aX56OrvxIxjQ9S0xL3H6xwgXciD2EcnRvd3d4h
XDN27I7VNfGF6Xlr6h833Bm8y9kH7nrh1BlMdbVUIn57Ky3Pw+OBruET2JZc
daOX2ltKjU0K9bTLTQxxO8w69+8sO2jVcDdzhAPNDHDLnz5LRHg8Qzg+PWif
YGAcDNM+tEbLdYORl8X+OA/fh8mpdYXve5rxDBL1M5sjEc0pFcrCyyk50dGp
cMc4XaMYNa2EdTrXdA0eGhm9tTRH77Bs2mOdY7G1JCOzC4vhEdp60OgAK8cA
LX3U+o0eeubRcMT1qJOv7z1sqa7lMWjCLwKpRCqXyRWKBaVSqQC/csWjxIQL
vn6hdgcRBoa716jvXaXq8LOqh4pG8FqdOM3NiXrbgtfrn/P0y7yQWvu8oOD6
bXcT21PO7o8vpKFfl7DxxOnRMalIpJRKlIp5hUIqlwMkaAsKxSIc+H+blXn3
VNxZ9yMBVntd9U3sYBttVDS3/7zeeIXW1p82GP19veGPGuZrNpzy9E8Lj4tD
+tU9fyVg9cqFQqVSrlyqRSZ4FArlnxUDW9dRXlyfn/P2TkZ2fOKlwODTSM8o
V/dIN6/TPkGXwk9ejo1PiTlzIyn14bWM1tqPilmxUiZXyqRS2YJMLlP+B+y/
appHHud0j7MJYxBhmITv62hhtGCgT82srq4hBn1qaFA0OSmc+iqcmpkXSZQy
BRBIGASxAAL+7+ilkk4PiKd4kq8D89PD8plx5dyUUjylnJ9VysRK+VKq8nnF
Uqzf+lIuMrAQnOBf4CslX2TzkzL5tEIGjkmsWBArpBK5fF4mX5ArpIpF0r9h
5EtS/EX44gKxXCaSyefAoS8f1XKk8u9Q39f/QF4ucGXFQtm8SCZbkH9Xsu/0
/9Q/Aart9CQ=
"], {{0, 32}, {32, 0}}, {0, 255},
ColorFunction->RGBColor],
BoxForm`ImageTag["Byte", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{32, 32},
PlotRange->{{0, 32}, {0, 32}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJyNVnlUU2cW78z8MdPO/GGt59RacStgoGxhk1VJ2JKwE0A22QwJARJCWEKA
rGYhCUnIRthRFnGhjtqKom2ncqptrZ6q7VRrxVotQhGRVZK3ZV6IaJ1Oz5l7
vrfkvZvfu/d+9/t+v+1FFanUP7/22mtVf0NPqYUcHJtdyCWvQ3+kM6voNGYx
hcisLqYVs4OK/oI+3Pb8sN/bbDYIgmAYhhwGQhAAgSA6VgDrMmC1WK0WAARA
ED3Qm2cAuLL62u4JOhwhAB32v/3GYBj1gGx/ZIgNdYCBhYXZCcCyACMQgNhA
xIbA9oG+XfOCYBts9109v3zxX2AIsnpCIAQBIRgNCwatS/OTX4+dONwh+f76
pyD49BmwaLEuw5YVBABsqz5rSTiGvQAwYkEQ6yoMGooD9hWzlwcAEMiyvPDw
s9EOcRWJmubRWJF09dLhq199cPXz4999efr+rcuTP98CLYs2NCcYRFFskA22
2mAAhOFFGFlCEOCPEoFBEAGeLc6Mnz+pbBbg64pd9ie8VZzipOXHaPgEvYCk
5kQqOPENjJTTRzsWZn6yLD94dP/bmUf3wKUF2LIIQk9A6Cmaxe/wV9OBITSk
pemfD7fxKgvcTQd8TSJvWYVrS52XscHb1Oijrd4pY2xtYnszcjzSojFKXv5w
X61amNPUkHvp3MEfbly4du3swuIvCLKC2CfpZVUQtHgraI5zloXvx07ragoD
qambTIKAdrGvhLmZV7JOVPqmjLkJBZcw3xOx3IVsLLccm5fwbmm6WyMtvITs
KWeTDKJMLjP+X6ODMLRssT5Dp3Ct/mgZAWQF+unOxyMnGTrZbikHqxeF6XjB
zTVeItomKWOjoWGngLpZUurcVPl+XTGmvtTDLCcqqvHFJGcKcUdG2DucfT4q
Nr48y5tTmvzjd1eslkW0k9eyQLt0eXb6+2NDTJMxSC5x6evCD/cltTaFi8td
FAxnXS3mkCzYxPXTc3x0HF8dJ0TLwen5CRpOQj5ua0WKe22WT32eV0OBFyvL
Yy/eWcAqvH3jCgJb1/DR6+PPLxq72pOHBsndnaThIXKPOUKvwBrFnoZ6TBPL
Scd17RR7q2tcG/dv4WY75+Pezo7aws71K47dUUl252R58wp8ypK2lia7FpPc
4wN28Cqpj399+GIWlubvosEP9GQZVOnDA8xeM1kt9WnTerapMAaxS3P9di3f
ubvZu1sdoG0IYKVsS/V/s6owWMTeIykLrM312Bf5rrQsvDbXL9H/bZLHhngf
p93Y9z4Y7kcXtQP/0f3rxwcYH/RXsPaHqUVxndo4vdRPJ3HVN2H62vH9bbEK
vmdfO+70MNmsiqUQnWjxLkd66a36RDU/SMkNL0raruelNdJIezCbfdb/NcFn
S2KUT3V96dT0pAN/9td77Xoahx5bX+6vlwa0iLDdquAeZWBbc8iFEcbF841m
XWqHKX5oKL3NENdI9W+k7jKb0kfOl547md9rTKHsdaFl+qdFentu3OC1/vXc
SO/8LFw+Pf3e/XH7mrKBKwj48cdn88ghwkoPDd+7Uxk6ZIoZNEY2Cz1M+tjP
PpOdPy88c6p0oDfZ2BRVmevWWBJaV4FrkiV8eLRUWR+djt+UQ8JEYN+J9N2Y
FonJIPrGRvpVcRhTU5Or3WNZsQFPZh53qmnSajeDJOBoO+l4Z1ybYpde7mc2
xl0cU164IPvkXH2vOUUl3FOQtEXAxKvEOZXlOC4rhEJ2oad5leUEE8O2dTbT
GIW4yDBMUjy+p6dzeXl5delaQOTJ5L3L3bJkg9C3z4g/0hF7tJPQ0RzSZcCN
nKYdOVzG4xIPtlNEDbvrawLpeW48Nk6nKdJoCorz3POTnalpPvsz/BmUaI2Y
lh4flEgIk4oFd+7cgeHn6+vRxBdnj1Xran149K0asb+Ui1HyPVoVYX0dxMFD
iWpFRDnNs1lC4FQFKWTEenZgBd1PKCK3tpdTCnzZtAh+RVJxzu46dvb+3MS9
qQSl/MCN6zcAAFrbg4BLY+ZufZSR75kX//cGlqdK5CviuAmrsW06gka5S68K
0CtCukzxrboMuZgk5+NkgiiVMqutk13NTpY2FDAK4tMTQjMzCPSS/d1d7XfH
71qtALpZP4/eMnfmFM+kw+rlAdI6PKccq5aE8qq9ucxAQS2urSVBI/RuUwVr
m3B1leFcRphJRpTUhUj48Xl5YcFBLrsD3cJ83NISiEIh/9OxsenZJxaUzmAA
drAAujUsTp88wdG2eCiaAge7SlukiXJ+CJeFldfHkQnvc8qi9EKcUbKHuu+9
nFRXIQuv5UWwCrZX03fFRu184/U/OW/ZmBQb0240P5yYWkY5FYKs9l3eCqNE
s7pLr1imRs4JDa3hLbpdxhZCV2titznWqCLIuYkR2B1Rgc5SLqG+0o9Jc2dQ
/RWiBK0ssqHSq5LimxTp6rxlHQ4XUM1hfHP9i4cPbn9z7fLSwjwEokyG8ibk
wLeCj09/JJbIggcHSO2mmA4zqctM6GlNryuL9nd2cn57HaskUiogtKjI7TqK
WZuvkUc3VnlIOKGUNExM0Oa8TOI/T/SfPXPw+ICiv0f1zdefAxarnaYdHIn2
Pzx/brRFqYxtNUS1GxMHenMPdWb1d1Ep2eHbNqx3Wr8uNgIjEWQe6W9UiSlN
Ddnm5jR5o3+nNvpAFTYdtyF5j5eQVSbn5rc2FyrltIPdmke/PIDslPKCfq1X
vjpmNuV3mdNUB2K6jfkHO2hyUQ4R7xni67cnKCQmwp9ZmtZYV0gvTOHQMxtZ
MQp++GBHglbgnxe7juTzbug2p6IErE5KFgsyteq6r69cAtH2gZEXHxj/8Uut
iqKWJbNLAqk5vhW0qESib1jQ+9TCIrPB3GE2tpnUrUZlX5f5/KljpuYqQS3B
0Jyok+Kr8nfuDdse7PRWHgnLr46r52QoZNU3r19D64MqoBccvDw/2dPGE9bF
MQtD/V3/kRSNZdDz6CWU4eHh2dmn8/Pzc3NP5+ZnFxfmAav13t1vDVpuRRmh
lhVVVxqeH+ceuO2NTGJQUW5sXlYUh00f+fDMs2UL9Jv4Ueodv3W5SZgvqklN
iNiJD8KcONZ3+/a/n87NQgjkKCQ6WWhDW9HegJBbt27qWqTM8sxyKpFFiYrb
7UzEB6WRk1Uy/sipkyeGT01MTK3JqucEBgLLIx8dPdgpVEoKCnKCDRrWzasj
K89+RdUgaBdPCLpeUMoGV1UUAACTkxNjY5+0mtRcDiM3K7mwYJ/ZbP7p3rjV
YnkyM7u0tPxcljjCX52MmZnHH314qN1cIxbsNaipcl7e0KDm4cQPsF1E2b3Q
MOw5w3aphl5RRTozM3Pp0uW+vr7R0dHp6WmHjkXW7KWsQiFAu8p7cP/W2TO9
TTKqmJ/dUE0uKozsH9IuLj1+jvwbc8hh9MZqtc7NzaFbMWhPDnbo5BdfeUVi
oR+CgOmp8YFDyuyMYAaNJBYXagw1N7+97FCn/1PyOer8O7RX7IWototw69LN
6xfLS9LTE8OrqrJULbVnR08sLs6jcaJlfynj/z9Dwf8DjJrXkg==
"], {{0, 32}, {
32, 0}}, {0, 255},
ColorFunction->RGBColor],
BoxForm`ImageTag["Byte", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{32, 32},
PlotRange->{{0, 32}, {0, 32}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJw1k3tUE2fexyEXZNuqba3Yi6h46WohISQhIZCQAHI1gIjc1GrxWrcWXVvX
2rracpN7uORCyGQyk8xkJpkk5B5ynYQShCCKitbubnfb49lz9j2n57znvH+8
f+9gd8/5zPc8M398fs/veX6Tc/bqsYu0tLS0LzKpONZ5s+z69c5bzW9SLy1d
X1y+1HXhfG3XlxcuXbhedJZOfdzzn2djDTljKjwwYnLfg5x94GyP3k7R/Yoe
0NEN2rtBogckegGiDyD6QWLAYB+E7MNG5yjiUZh9E3hgyjqntoe0s1HATRq8
SWNgGYs8tJKPZxeee5f/Mo54h2Bnv8HRpyd6dJb/AFg30L8CtPTpLX06vB/A
7+ktgwbrIEQMw45Rk1Nh9kziPqXFr7bNTdtDOmdU70nA/kVzOIXHVh3zjz33
fxhDfIMbfnu/3tqrw3t1WM9/2dDqLf16rB/ABgBsUI8NgdiwAR+BLGNG27hp
dgJ1KTGPyuKdts1p7UHdbBh0k0b/91h4yRpbsS+suZefK1DvEGQfoDYJmHt1
SK8O3UitqW8GuQeYN9CjAwA6qEOHAHQENI8azGMGTAFZxo22KcShwlxq3DNN
+LW2wIw9CLoisI80h5LW6LIj8dCbfDyJecaMxIgBG9Cj/QDlfIXONEABIK/S
NAggQzpkFDQrIGwcxikUMOUnJhG7CnNqLJ5pq3/GFgAcAcgVMvtjttC8h1yM
fr/64MGzV37biAEfotrXmynP0CvngM44qDNSeW/DbxwBTWMQMm5Ef2PCiE0a
rVMmQoXaNZhrxuLR29xGp4fw+qPxxOpS8seHSy/XH/3604sxzDdsdAwaiHug
9Z4eGwTMg3qUaqFfaxzQmgZ1yCBgGgHgCRDSwLAWhmeMRh1iglDEjKOYFbMQ
OG61Wgm702kPh3xLifD6UuKXtfu//vDg//72+P9/ea6zODWIRQkhEyA8ZYA1
sFEDQWq9QQNCWhCeASEAMphMIIGBYTcWc5nnfZbknG0pZE+FbCth+0rYlgrN
Pgi710jPi4XAz6nwP1fJ/1lb+PXp8v++2CiRCHoibsJvM7ktoJ+AQg44YAF8
uC5kM8TscJQwJJzwfY8x5YXWAsbnQdP6nPHZnHE9bH4atTwnifWodT1mexF3
/m3e/Y8F78tF38uluZfL0Zcr8/98lPzXeupH0vM8ZF+fszwJoGs++IkXeuo1
PPLoH7mBx26QWj/1Q0/80EMPeN8+nXLqVlzA8uzMkgtc9iErAXMqYF72Iyt+
9FHQsh6xP487n5KuJ3Hf+nzoxSL504Pks5DjsQ9f8yCrLmhlVv/AoXvo1K84
9SmHbsWhW3XqH7gMy04w6TAk7CDpAOOzUMwOxmxg3GFMuJCEC427TAk3suDB
7vvwVNCeirhWSd+jRPBpMvbD8vcpL744Cy/YQNKijZjVYVQVQVVRVBNB1VFU
TWLauBWIW3UUJDETcwBRmz5sBSJWIEboSTtEOhA/NoPrFKQTm3eji35LKji7
GnWvUS0shH9YTiTdWMIGkRYgjGnnEI0XVnoME3PQRNA4GTIpqRJxbDqOaeKY
MoYrIxZ1GNeEsOkIro1ZdFSJhNOE6xX3/vzHeY9l0Yc9CFqeRGefJzx/WQz8
tBz5eXV+3omShCGK64LodMCo9sEqn2EqCE1EjFNRkzKGKElkkkQnSEQRRRVh
80QEU1JtxvDpuFUbt+uTHkQ72XPrxqX7c5aU3/woiD+LEj/GZ/++6Pt5ee7l
amxh1kSdAInPxMzaKKKJmNRhozIMT4Th8TA0HoEnYuhUDB0nzeMkPh7DxuP4
VBxXxXF1gpiedwBJN9x99+rVa5987zEuOsEVN7zmR5+FrX9NOP++4PklFUq5
jElCN4+p49RWjZMxSmicmNOPBPUjUXjcqenX99/wGUaCiMKuuRtFR0mzgmon
jk2FkDE/PEoS2kuX20+fawriqkd+ZC1gfhqyPIsQL0jHXxc8/1gKLjvApEW7
YNYk4KmYYTxiUIShMYeqGxn+Guj709eXOpori+9cOXf7yplbV9pNyjsxm5q0
KuOEGhy51X2t0zY9fKypUloumOr90msYdRvGXYbxIKqK4ZpFJ0RdxIJdH8c1
JKqJwpNhgyIIjM4Bo37d0Kx2EFP199z6TMA5WHAgRyrKLyrOlR+RDPXfQIEB
VHevtly4f9e7Ym7uvpzst99+M2/fTkHuHkFeTrU4f3rgKy88Rg0kddcxOzU5
yqBpwgsPeQ1DfnDMox0lNCOzeoULUiDqvu4vLyq+6/r0Ukf2gT2b39l6kL2/
srb4eGvVB9nb6Zm0Awf37N67s1hU2Hmy5frn57+6dmHoztWYA1yNWNei9vV5
bwyfCZqmqIH0QiOEfnBG2XP7dtelz88O9N4kZoac2iHXzLAPGvj62tnNb25N
o9HSMumMLYy3sjbveHfbpi2Zuw9kt7fJYe2o32qIus2k15ycwxcDWCpoWY3Y
1+KeCKrxm5QOcFI19O2NG5fbLrSVn6wXtcobP26+e+tzcLzHMNlHaPox1UCt
TMRhH8zNO/C7Nzbt3btr+ztvb9m2tUCYrxi9G7DOBBB1AFUF8OmwDUi44KQP
XQoSK1GXA1ZoprpvfnO1qfPk4fZjsvajkvajxW3Npa2N9aeaTl4+efoPp25/
dQWe6lX2XQfH/jz87RdtR6vv3L5RWiHhy4rO//H8V3euTYzcdUBTIXwmYgOo
w4k7oXmPKRmwLoWdXTcvN59vLT/RUHKiqbiDMjeUtNRLjtdLWuSyjoaKU42l
rTWVrXWfdp1RK74xq78zTH430HvjYtc5+cct9Z3tTedPNp/rOPPZmZvfXNOp
hnB40oEq4y54yYss+4mVsKe0tU7S0SBqr+c313CPVglb6opajhS3yEta5eLW
ellHo7TtSHHbEVlb7fHTjWcvnTh94YT842ZZO1W6qfqTtppzp+QXTzf+4czx
K5+cv3bx6q3Pb969NqnsMxunbKjabddvP7Rzt+Cj3UV5O7kH32Pt/72Yl1dW
xK2TFdTJ2NUSXq00V1qYWynmHpGKGktLj5eJj5eL26qLqb+isaLsRENlZ2vV
+ZO1n55p+OyT5iudrVc6O66ea/n01OWvu/7UffPb4e483q6DnOwDrA/2/v69
nTnbdua8s+/Q+4cK9n7E278vL/tAXvZ7u97atmtb1r6sd/dnZR/c9f6HO/fn
f7jnYHaVXCys4BbVCOs+bqg5UX+4tbrmZF1ZU5mwSpgv41SfqC0/XnHsYktD
44d1dfuqqnIqKnJk0l0SyQdSaXapeJdUspvKEtH7JaIPCgU7Obz3uNwd+ezt
bG5WAW8HtyDrWBNfVn6gqGSPvFlQJWdX1eYeOcqRN7KlZXvEZTkVdbkVcnZF
Q4GoNF1QnM4XpvFEDG4RnSei80VMoXCTUPAKYaZQ9FpR0dZCwZZCwRsC4eu8
ks188RvCki1FxVtLxNtKS3dIyrNkh7dXV2ZVVW+vq8uqP7JDfuTdhobsjhMf
njp9qKycKZYwRCK6oCiDL2Bw+TReIZ3Hp3O56QUUBek8Do3LphWw0tl5aSxW
ei6blstOz89nFOQzuQUZAn4mX5ghKM4QipgCEV1UQqdspVJmWUVmdV1GdUNm
aTGzuJAp5DL5BUweh8HNp1NwKAMrjYKdl87Kpf9Gbh7tECv9Nz5ipeexaWwO
LZ9L5/LofB5dKKSLRIySErpEwpDKGLIyenklraJuk1TIFPMzijhMIZspYDMK
WYyNZKfzWWlU8lg0DouRn8fIZzHycmkf5dHz2IxcFp3FpnEKaDw+g1/IKCpk
iAsZ0iJmWQmzXMw4LGVWlTEry+jVlZuqa35XJ8usLNlULswo52WWczOl+Uwp
hynhMCT5dGlBhpTDkObTS9k0CYsmZtFFucwSVoaYvamUk1HGZRwWZFSJNtUU
Z8olrzXIXm8se/3o4deaa95oqdvcKt/S3vBWx9G3/g145Pw2
"], {{0, 32}, {32,
0}}, {0, 255},
ColorFunction->RGBColor],
BoxForm`ImageTag["Byte", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{32, 32},
PlotRange->{{0, 32}, {0, 32}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJyllnlMVEcYwE37T/8xaZr0SIxWghgjlBKbttQWKdUieBAB8eCSJd4cBtAi
SMDaUkWstVHEArZQaMGjtlJARVkFFBSoRcFlUTTh3MXl2N333pxvod9DsEtq
ccHJ7OTtezO/75vvmrEL3+G3+aVp06bFvQKDnyreIzZWleD/KvwJiI7btiV6
00bv6J2btmyKdQ1/GV7OHv0pz5RSSZIQNBgkIkl0rBMBC2ZkNiMkICogpkyS
lLnSZJrFYqH/NjbWOSEwSEyWGIcnRgijU2qyLJPxDWMMcinFg/1dWk1Dq6bR
PNjHCYYPZPJtPB/YCEZZ5j3dHYfTkgN8PHyXeeRlHePITMmL8jEWKZO6u9tr
aqtTUhLed5493+41u7emuy2YX1VewhnFk9+CFZ8igjmT2tq0ufl5fr7Lnee8
4ThruqPd6/Pt3owOX6vvaaeKCIoJtV3MUz6sEsAb2EywqB8wpR9I9fzYyd1l
hovj7K1bVEGr3EuKC2QLR4gjIiObJVjx2QhfIFhCfKjqSmnIyoV+n84LCfYv
U1eEBq5MSYpgFL4yRDiiU9FffMIHP8hDXS11x2J8ftuvenD78vXaytU+7qtX
LGysU1u44gRQZgp8iXKORXhAlOsby8u/cL211+1WXsKeiAB/97lL3pu5OzJI
367hDEQA36Y9WPMRYRyMA7pRqq8tup/kqImbcWy9fehnc4I97Ncscli92Ck/
64Bo7seYT4EPnREoEpxSYqwrHDy4oG+fQ3aoQ7i3U7zKa/sq10BPp4gw77u3
a2U+bGOoWvEJYkgZicyY2Nd8rj9niXTcpTLJOXalfVzo8sStvoeSVPER/rkn
0kfcJEoEIaV0wIbRc/mgvsQFCeZjC2fm/u7Kx2WhUpFrX96HZ3c7b1w2d/O6
Twqzkr//entEiFdLw2VGBwUiilxZDl77v+y2yi+MmIjA9MSixKGoETTp+HqI
+YL3/dNex3e7BHrNjAh0jQ52C/Z2St+j6u3SQJwKlI7wJWIDHyJoxGtQMUXG
dLj/mtSaIdXvNNZuay5Vpe5wW7f47aDP54YunRe24p0rxbkYDYhKyYIFNthH
QT/JS4opwkyQUK+x86bYeprczxEeZDZdPXI0eUOw57v+i+zXLrbPTNvZp3uI
sIQnTAZrPoeZSlhgRCHXIAuY0aB72Hit416J7lGxsaOirf7C4T2x6zw/WPbR
rJgwr+YGNVbyZaLSPY4PeTXKZ5DLsAuCBG3TX2Wlv1y49KO6LEf9R2FBRmZC
5OaApe/5uDkc3BujbbkjiFCy0Ij5n5ER4+yDR2couQAHDEGiqR8NGjraWmuq
r54/nZdx6JuC7BPFpwqKcjOO7I+PjQhO/XLXrRvl5kG9IgFDEI0BnsW3bk/U
Meg6ux5omMnMBPxIey8747v6G1eR0WDu79F1ttRUluxNjIqLCisq+KGvT0eh
8v3H0RPwKWOm/t5z+Se1f9cjk7FKfTn/p+zmxoYhKFSSkeEB0aRvbqw9cuir
0GDfo8dT2zs1YNeR1cwWPgiQiZiXefjXkxnV6ksXS4vLSop7ujpkBpaDQm2C
zoh5oE939szPQaHeKfti9L3tjDElwp/PB/uz4SGmLjm1K3JDxcXf6+tqa2pq
KH0qH6IMrixQKOCOIdXcvJSWnqzV3uWcUxv0H/E2H7bQ8vMFIQFLzhRmVV5T
P35sUN6Peo8+7UqOUWQ0DQiCGRSglNrAB1fh4SFa/mfReh/31KSoe013KNTv
0SijY+FGR19CwNHRom2Fn4APWSAyC22+27BDFfBt4naDrouyCTKVPjPJJtQf
DltuMOhSEyPjVD51NdWcy5O9okxkfywjYhGROTcrLTFqzY2qign1nywfGpeI
TDhraqy+eC5H1w33H2btuxfjKxEIxw0EnygOiANdGIk2nrm28qkJTkyBcgTB
IQlKESOTviL+A/g9nZk=
"], {{0, 32}, {32, 0}}, {0, 255},
ColorFunction->RGBColor],
BoxForm`ImageTag["Byte", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{32, 32},
PlotRange->{{0, 32}, {0, 32}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJxFVQk0Ve0aNs8yz/N4ijJn/GWIkCIziRCODOFQIeGXWWSex4OQIQ2/oZAk
lELKnByd+Zx95mNIde/d/v/eddd69rvevdfaz/O+z/fstVVCYt3D2VhYWBJ4
wOIefNsGBgtO9hAGb7xuJFyH3ggLdbqRGAYNg5mGsIMPlf97HfX03/+mHP6i
/vxN+fmb/OM36eBfeOZvDP0Xiv4LzfgNAkn7iaAdHoF6+JW8v0phVrS2qmiq
Oft5z3xDfcIx5tGUBQx1Hkubx9PnsNR3aNIsEphGECe/A59wFJCZuHcA7P8A
9g+Iez/wzEMM9QeKfICkHKDAhnrU7FD2EWQQe1ukvWVg/9WLoZqMeBcH6+HZ
j5/xtHkUsIgmLWLJC1jyRwzwAQ3MIQnvdgjTSGAJR6L9+hdITjo4BCtx7xDH
+AHyo8n7KNIuiryLJu9hqPsYGqi1h6LsIUi7Wzjm6sz0zqtnNdnps0sry3jq
Egb4giUt4ymf8eQlLAnkXEQT51HEOSxplfj/+fG7+3jmPp5xgKUdYqmHWMou
hsxAEWgogI6mgFoMFImOAGhrGMLK2kpHY1Xy7dgNDHYZR1nGklZw5FUCZZlA
+YInH1UcCRRawFM2SVTa4S/S7gGwu49lHqDIlK0dxJdNxNLazqeV1Y/LK9+2
ASSZ+R1gooh0JI4ManUPjfgFBZ3QOq6gIvf45dg6gb6CA9aJpA2AsgHQ14n/
gLZ6pEX5RqZRD34CzH0iYw9g7iLwxKzCYmhwoP952wt25sZmxqFQ2PQacoe4
h8AztrH070RmSlYumAo2NlawpuTkbxDpy1jiGoG4QSRvAoz/4UhiBU/dJtMo
+4cgOYG+S2fQ3nxY0DWzttZWynA9ddVExu6UvKIwr9NFt4XlrW3C7jqWuYoE
LgeHsLCycHNxsbCzZhSWbOJpq2jCOo6wSSB9JdC3iIxtEvMbifn170W+kxkg
P0iOpzFpDPrg6GtTc+vAs0Y1QaY3LRUCDRQDTORlOFnjY2I3keDrexMzC7p6
uuDkHGzsnDx8de09WzjaOoqwgcF/xQJbOOo2gbED7O4AzC0CbZNARx/x/yTQ
97AUJpG2O/PxkzYEYqYscdVIzllZzJCfI0BP8pKupqa0WH1j29IG2u9KkIyU
uI7WcU52Dml55dG3H7cwlDUkfgON30QTNzEUUA5BYCDARXCUTRwNDdApP36B
mcHRDkjUvQ9rmzr6BieEeBzVxXWFuV2PS951VC8OsXM7rfKHvkFUNAxyXPW8
vaW9tQU7O7url+/Gd+wGkrCOJm2AwJDWsSAn9StoO3iyGOAbDswegwp+VjQa
gUbBk5g7RFKQzyVTeSELVXGICJ/bSYmGEJP+FM+aaB+ItKiRgU5cuH9qYpSP
p6uHp7v9+QtLWzvrGGADA6yhQYsABJH2DU8F6xYW2D7ip4L8DOYvgMQgEMko
wh4CjU665uGko2BrrO3hcNZWQzzdGVIWbH/DyVpFRtTewdbXxbm0IIfJpExO
TsgrKmbeL61ohpdUVgyOjb559z75bprn5YCW7r5tHGkbQ9zCHvEjsDgUgYIF
mDjq/gYScfmivZWWEiwqpDAv10xT0c9A3k5NSp2PR46b9ayJQQw0bGX5M41G
efLksaKivICQqJSYKERG+IKViaeLk7ycFBsHm5aewYs3M9/xlC0sBUVi3CtO
LKkvaO1pG387+m51wcPHz+GMRUtT9fDL8ZPqqurHuCS5OPRE+VzkBIKM1YM8
naprK6Nirj/saMvNypQUEVYV5HGESJrL8esqSFqZ6YsIC7Kwcabey8GQ6P/M
/1d/3kN4WlV5/P28yOrq9MzshISkiKcjvfDOdllpKX5WFjleTm+ITKa1Yr63
kY6i9DEhAfuLNk/6egnI77k3w82FuUL0FNy0BCD8Ag5mOsZGuiysvMHQiO8A
GcwSksBAfh7YnOtYnWlYniifHsga789+2pk50JmdngLlFzzGxcKmI8ILs9C4
+Yf8TSftP9RkBDi5jmuppyVCn3eWdeRAI3QkA1UFIi3ETnFzWEOUHc6YsbDy
eAZe/oLaXkKitnDE1bdtS2OVK2MlG69LN6cq1qeqlierNqYqi9ICuXj4uFi4
DcT57JVEtIS4TkoJpUYGmZsbCguwR9iq3PfWTnPUTDur6iHFEWkiZiMucOoY
n7K4MOiPur5mXNatuJyUgrry7Q8dX15XL7x88HH0wdxo8dzL4tnhwsXRktKM
a8KCfJysnGKcbNIC3OI83CqS0pWlReZWphL8XCmO6gUOytbHOH10ZR1khfx1
xB2VxFV4OGRFBdi4OEXkBfTP6pg4G3uHeiEX29dnGz+9qV56U7n0qnj+Rf7c
4L13Q/eLU8PUxfi4WY9+iwJ83BBxIVMNVdiNaGUFteOyEEslQRM5XhEWbg0J
QU0h4T8URME1ZQV5Thue4ODm0DWFRN0ODIx0jU8K35pp2JyqXRkvXRwrWBzN
WxrJW3yR834wpyrBJcBAVl1UwMRIT1NdSYybXVVK5NQJDRVZeQt9QzkRfk0l
CTCcnOxsgjw8qmKiElxsUiKCjucsuXjZrc+ZDwyUvRyqnproWwSdGcxbHM6b
G8p4//zO+4HUqf5UeGFAQYB+rodWbpTLcGduY0mSioK0hopcfNila142qfFX
7sIul+dHXvayYmPhkZeV8nc/Azovws9vYWbMw8vueN786cCDV8NVC+/+Whgr
mhvK+TB4b+ZZymRv3Otu2LNmWJCrbuAZuY4Mj4m+zJfdNyd7M4yNtQ30NZ80
Jg40xA603h7sTBnsvFVWeFVcSFpGWiI1yc3BUpeXg42Pl1dG6ljm3ZDHffnP
+wumxrvG+lNe9adM9N560hLxpDV86GE8LMJBT1si6bpdbw30ETxhAH59uPuW
leVJfV2lrtqI5+0xvU2R3XXh/c3Xe9punLM15OZk9/EyuRnrDFETA4/Lyd64
p/Vub/e954/zp151dtZF9DRe76m9VpByNjvFOi/tgrGehJfb6aayq+0Vfu21
QZ3V/vC6MFsr7dMGCi210J5m6KOmsK76sO76iEctkVl/+kiKC53Skk+74xQe
bi0tJ3ze3vjpw4ze7oxnj3PfvIJHhJkGBxkmRlneiTHLTnX0dFX3u6TVWBrS
XnsVXn25rfZyV/2V7oZrFx2M7G3VG8v9Goq8awovNpZ4tJZd6aoJaa4LNzSC
aKpIpic7Fd33d3M3NzPSaqiIb22E9XWlT040hEKNTW3Ej+vxmpyWsLNS0zkl
4u9rcjPGPiXeNu2W3Z8p9rmpDnWFPl7OJld9dRtLL9QUuJfnOpXm2JVk29cV
uVYU+Zubavi6m1QWeRUVXEpMcLUy1y4rDGusieqG3x58XjQ3fr+hOsrZVUdR
QUBBhl9DVUBNhUNBkU1GnkNFg0f9BL+aJp+ZqfQJiLzbpZO59+xKc91rH7g/
yLHNTbfISTsTEWxsZiiTknC2LM8p70+b1GRnKwtIdoZfXXlYW90N0CLEbMXc
SG4yzPWKt0VWkndVXkDGLUdoqKWDo5aJqdQFF21ff3MfvzNqCtKujicjg3Vj
Qg1vxxmlJ5nnpNlXlfheOnci2Ot0Y7l3XZFLRZ5DfpabpZlqxDXr0jy/ysKA
no478yP3pp+ldjbEddbHjnbffNt/a6g9+ll7wkBLYvOD4I6qsIc1kbDrDpes
9WqyQzrKg+uLAwsznRMjjaFXdCKCjM11ZHOTvDvrr8IrfBuK3WpKQ87Z6AT4
WLXWRLZVQh93Zox3xY13xw+3RU8PJL17mjzZCxtsgT5vgo7AY8cewgabox7X
QIuT3WqyfIfbY8d64l8+ShjtuQXGuC7fMy7YPDnKqb44uLbYu6HEvSLfuao4
wMfd7LSBUlNV6EBr1Iv+gqG26yMd0S8exow9ip3oi3/VG/eyK7qvLuhpE3QQ
HvWkMfxFR+x0350X8Oin9UEjbWFPW6F9jWF9TWGtpX7wyqsddaHNFVfg1QEd
dYHN5X7NVdfSk92goTYNtUEd9SGD/fmIz8/W5nq+zHYtz3auzXWv/o1PU22r
7x+tf+j9MtO5Od//benJ5mLfp+mW5fdti2/b5iZapkZq3gxXvx4ufz1S9nqk
cmKoanq06f1E2+xE+/xM3/vpnrdv4NOT8C8L4/8BwYKA+g==
"], {{0, 32}, {32,
0}}, {0, 255},
ColorFunction->RGBColor],
BoxForm`ImageTag["Byte", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{32, 32},
PlotRange->{{0, 32}, {0, 32}}]\)}]Out[6]=
For a specific example, give the probabilities of the most likely label assignments.
In[7]:=
trained[\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJyVlllzE1cWgGHmJTVPgdQUAa8YhrHBBowkLNmyrNWyZe371i2p1d1qdatb
+756lRdZMrbBgA1eMMasBoYtLAFMErJMVVIzU5WqecwvmUvIzNO8pOv0rXu7
ur+z9LnnnsNIUI//Yc+ePdFPwKD3JEWRiCdt+BQsTEzU72MwdJCJYT4swkX+
CB42/3Z/mO/du3fP778+fPRR/rf8/6/t3b9/f1dXF5fL7ericDjsjzeLw2ax
WGw2m8vj9vTyBcI+IHx+D4/HZbNZ7R0n2o4fO37iryfaW4GA+bHWo61tfwGT
1uMfxvaOtlOdJ9kc1v7PPmtubqYoKhaLxBOhaCyUSCRSmUwylw1FwpFoNJ3L
jpTHZ2rV2bna5NTE6GgpFKYh2KbTK/TGISA649CAUiIZECi1/RqjAoyDKonG
OIT6PbFU9PCRlvr6erPZYnfYUAyiAr5YNJYvlgpjI/F0KpaIx1LJVCGXHxku
jo2UhvPpTJzwo07IrNHJ1FqpQimUDfL5Ek6vhDOoEWnNg2pjv1wlVOqlHp8z
nAg2tjTX1dcZjHqL1eRBHD7CEwzSmVw+nc9FE7FQmAnHIrFUIpXL5kvFfCEb
iQYJArPa9Eq1cFDZK5FzBVJ2t+h0j/j0gJqvs8j0ln61QaIzy924lY74mw43
1TXUma1GB2RDvLAXhTDcGwyFw7EoRZMY7iH8Pj9FBRga+BJPRGiG9BGo0aSW
K/gi2Vm+uLNb3MkTneIJO2QKjsYo0Bj71Hqh1iS1wGoEdzY21dc31NmdVtjt
RDE34nV6PDAVoCOJmJ8igEYUQ3DChxM4UMcEyQBNAKUGo0om7+4VsXh9nT1i
TreY3SM6I5GfHVR3K7W9Kp1IY5BqTAMmq7a+4RDgA+PdCEQQKO5zYxjCBEPx
VBIA3R6nG4FRHPFiHsznJSncT6IeBNLqBgFfoRIbrJq+/l6BtFvY3yORd8sG
uQOqHsDXGuVGu8bqNAL4Rz7idQVDVCzOxOLhVDoNoh2OhoBHrg8qIMhlBxMU
cwEHQfBVatngUF8giK9uruZHCyiJBUKk0aIeUPYOKHuUWpHBMgQhDjcKNzSC
+NRDLgfuR7P59Hh5ZKI8PjlTmaxWM/kMReEejwPwnbDNCVlcbividUCQ2WbX
BRj0/sM7P//753/+/K9vvvv6ze6rq2uXCco1oASJKrI6NF4C8fmxxqYGoMKN
uuhIYGxqvDo/V5mbm7+0vLC6OloeCzEE7rURBEIHyWiYwDEnw/jyueSFC3PP
nz/+6acff/j7t9++f/v9+7fv3r549/bl+sZVyG3WGCQ2p9ZHonSQAvkD+C4v
zESZ8emJ2sK52vzC8sa1levXx8uj+XSkPJIaLiaXzle3N5erM+PnF2v37tz8
5uvd7394//r16wcPd7ZvXNm5s35z68rW5tVXX76ozU87XQaHy+insFAkCPgg
Pi4EJoP+0kh+ujK9eOH8pasrEzPlYjG9UC3f3lzeuHzuyc71Jztbt29sPP3b
/W+/2n3+7PH2za21tfWlixfOzU2sXK4sX5xdvjT/6NHOvQe3A4zPi8MEiTGh
wK/8OhgkD+2LxUPFUm6mMl2eHE+lo8Ds87Xy+sXa2uLUvfXzW1cW7t3aePPy
8ZOHd6uVyUI+l0pmgsEg5ffGo+TYcGphrgz8fvb86Xh5DCe8gP8xPvX1dQ6X
3evzgNxLJMOJRDQUplDMiaOOQio4Vy7MjcSXJjOXa2NPHm7du7VaSIdIwoP7
8H75ICiAvT08p9WcSQYvL1Vu3d788vXrtfVroQgDVFC0/zf73TYPYsdwiImS
JI2jGCzt5wt72R6nKRX0xSjXaIZcquSWz4+WIniCQIrpmMmgbWisO/Dn/Z2n
OpxWYz5Bba0vvnr16M2bNzv3H+WLBbANvagL5E9jYwPh9/pJDw74EcJPIZBN
b1T2d3ee6GOddNm1NGYbSxAzBTqG26KQZbFUWpiYxGyOzva2tqPNAzIRApsm
8uFrV+ZePn+wu/vm+YtXtbkaTiAwbK+vP9Tc3BQO0+FwgKLQeJyOhH12vQLS
K2X8rrPHj5i00mwAWR1OTYawmNuWI32TuWy1PEkTpEmvlYv4uiEZ6bVVRuLX
VxdefnH/h+++evfV2/WNNbBbEcQFinNLS0s6nU6lErEoQxMe2gd5HBoENtot
OlHXyZDLeG0sv5GIXqHIVZy8HAhOYr4FMrSEhycoxmHUWI1DNGqdKoZBfO7d
Xn/7+vHu7ssvnj0tlfIEgTc2NgF+qTQ8OjY2NlpMhUjKY8VhHWRVWXWqgEX7
eGbiCk1lpNIndOyVP7zigNJy6YzesGR3lTEUtRk1g0LEopgZDq8sTV9bPf/o
weaL5w/e7b6Zna0EAlRT0+HDLS2xRCzAkKjL5jarHVqpXSM0DQkjsHP3woV/
LF7cppgdin4fjD+FkRm1MqiSZ7zOCOoMeCHEadENiglIN5EPVCbi1cropYuz
2zdXXr54Mn+uSgeDTc0f+JgfFUr4XHa7gNuhELOsWmGadr1cW/pl5+4vG1s/
zi8+SMQWTbphqZjo63bKgME6HHUGaZwJ4JjLGiKgVNgzkiPHR1K12tily5Vn
T+6urV5KpNPNLS1NzY0kQ5jsepVK7rDrCcxB+aCVauHdRuXLpenVaDCpUxn4
bAn7uIDdKuC19/eyNLJuvVbosCkxxAZOS8JjjQTcmRg2WghWJlMLteGnD7dv
39osjo4cPnIE1B8v4abCBEkTuUJ6eno8lQwFEf0UY4y7hrQSjqznpITfKZd0
qxTiIZVIr+/XqYX9kjNDgzyTXua0qlCXiSaggM8RD8HpCDI1HN/ZvrJz98Zo
eeLD+d5wyGTXORELqHjZbGJiYjgeDRiGBIhRqlfwNJpeg6ZPJeMpxFxNv1Ax
ILTYtG6XyWoY0Kv6dKpeh3WAwMw+1IwhxiDloHB7OkasLlfu3N4sjoyA33vw
0AGFWmq0qjxeeyRKFfKJXCYU8LtBYfF4LGatGNaKIHUfZJLBdo3TocdRiCG8
MZrA3WazTmwzS2BIATtViMfgw2we2EQHXLVqcWNjJZXNgN37+ecHxLKzaq3E
bFURJJxMB7JZUIICyVS0WMoSXithlTOO/hCmiVDOKOVO0GiS8RVS0VwyhCEW
h01hNfVbjErIaXW7rYQPjoSJanX87r2bxVIe7K/PDx4QSTvlCq5WL0VxRyIV
yuaSoNHKZJOz1elkgvbD6qBLHsVVCcqWZuB82BslnKUkPTWeCQQQFLVCdo1e
N2SxmFwuB00T6XRs/tzsg4d3C8XcoUMHD/7Kl8rZKo0Yw2GgdLZaGR4tpTLJ
mdnpsYlhErOS8GDIq4oSpjQDZYPuJAWVEv6ZcjYcIXEcxrwOECmn0wG7YIoi
s9lMuTxxY/taLpcG9Lq6QzI5T9bfo9UpaMY/NVVeXVudv7BYGCmBnrA6V4uE
SNJr8bsNNGqJBdwxCslHyeEUMzmaTSYjfj9GBwiv1w25YA8CTlKmWCpNTk1e
31qfnplsaGj49NN9x/56+Nixo8ePt7LYnT09PJFEJBCLurp5/D6BoFfIYbHO
nDrR2d7KOtnGOd3OOdXBZZ3md7HUg/JeHvcsh8Xjdp3tOtt+sgN0xZwuDl/A
7xMK+uUSgYC/b9++/zbZv69L/9Mnn/T1Ajzgcxrq61tbW48cPQKk80wnkI6O
9lOnTra1tQH+fwAN6ImN
"], {{0, 32}, {32, 0}}, {0, 255},
ColorFunction->RGBColor],
BoxForm`ImageTag["Byte", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{32, 32},
PlotRange->{{0, 32}, {0, 32}}]\), {"TopProbabilities", 3}]Out[7]=
From a random sample, select the images for which the net produces highest and lowest entropy predictions. High-entropy inputs can be interpreted as those for which the net is most uncertain about the correct class.
In[8]:=
images = RandomSample[Keys[trainingData], 5000];In[9]:=
entropies = trained[images, "Entropy"];In[10]:=
Labeled[images[[Ordering[entropies, -10]]], "high entropy"]
Labeled[images[[Ordering[entropies, 10]]], "low entropy"]Out[10]=

Out[10]=