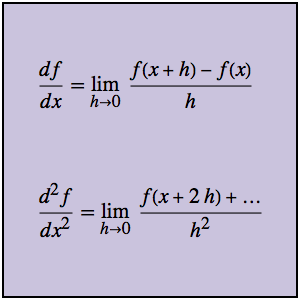Evaluieren Sie eine Ableitung mittels Grenzwertdefinion
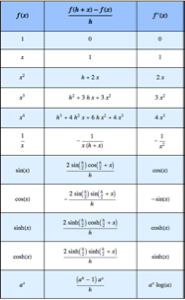
Mit Differenzenquotienten berechnen Sie nicht nur die erste Ableitung, sondern auch Ableitungen höherer Ordnung auf direkte Weise. Behandeln Sie zuerst die Funktion g und ihren zugehörigen Differenzenquotienten.
In[1]:=
g[x_] := x^2 Exp[x]In[2]:=
dq1[x_] = DifferenceQuotient[g[x], {x, h}]Out[2]=
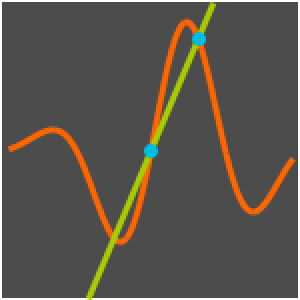
Berechnet man den Grenzwert des Differenzenquotients, ergibt sich die erste Ableitung.
In[3]:=
Limit[dq1[x], h -> 0]Out[3]=
In[4]:=
Limit[dq1[x], h -> 0];
Simplify[% == g'[x]]Out[4]=
Die zweite Ableitung kann direkt durch den zweiten Differenzenquotienten angenähert werden, ohne je auf die erste Ableitung Bezug nehmen zu müssen.
In[5]:=
dq2[x_] = DifferenceQuotient[g[x], {x, 2, h}]Out[5]=
Wenn  ist der Grenzwert die zweite Ableitung.
ist der Grenzwert die zweite Ableitung.
In[6]:=
Limit[dq2[x], h -> 0]Out[6]=
In[7]:=
Limit[dq2[x], h -> 0];
Simplify[% == g''[x]]Out[7]=
Der Differenzenquotient der ersten Ableitung ist eine andere Funktion des Differenzenquotients zweiter Ordnung von g, ihr Grenzwert ist jedoch auch die zweite Ableitung.
In[8]:=
dqp[x_] = DifferenceQuotient[g'[x], {x, h}]Out[8]=
In[9]:=
Limit[dqp[x], h -> 0]Out[9]=