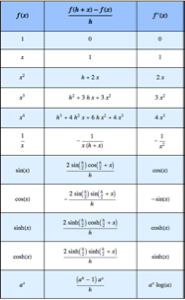
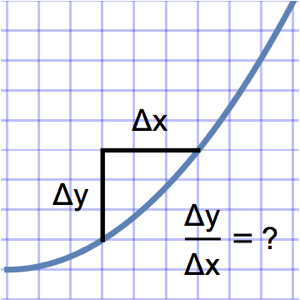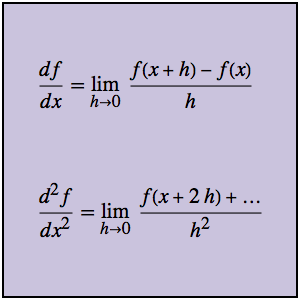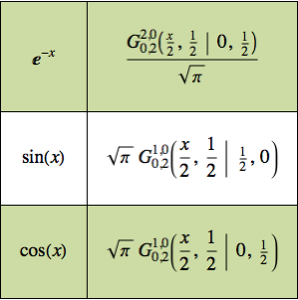Ermitteln Sie die Ladungsverteilung auf einer Kugel
Ermitteln Sie die Positionen, die das Coulomb-Potential für kugelsymmetrisch verteilte frei bewegliche geladene Teilchen minimieren. Dann handelt es sich um das Ladungsgleichgewicht.
Geben Sie die Zahl der Teilchen mit n an.
n = 50;{xi, yi, zi} seien die kartesischen Koordinaten des 
![]() Partikels.
Partikels.
vars = Join[Array[x, n], Array[y, n], Array[z, n]];Das Ziel ist die Minimierung des Coulomb-Potentials.
potential =
Sum[((x[i] - x[j])^2 + (y[i] - y[j])^2 + (z[i] - z[j])^2)^-(1/
2), {i, 1, n - 1}, {j, i + 1, n}];Da sich die Teilchen auf einer Kugeloberfläche befinden, müssen ihre Koordinatenvektoren alle dieselbe Länge besitzen.
sphereconstr = Table[x[i]^2 + y[i]^2 + z[i]^2 == 1, {i, 1, n}];Wählen Sie zufällige Kugelkoordinaten als Anfangspunkte.

rpts = ConstantArray[1, n];
thetapts = RandomReal[{0, Pi}, n];
phipts = RandomReal[{-Pi, Pi}, n];
spherpts = Transpose[{rpts, thetapts, phipts}];Wandeln Sie die Anfangspunkte in kartesische Koordinaten um.
cartpts = CoordinateTransform["Spherical" -> "Cartesian", spherpts];Ordnen Sie die Anfangspunkte so an, dass sie der Reihenfolge der Variablen entsprechen.
initpts = Flatten[Transpose[cartpts]];Minimieren Sie das Coulomb-Potential unter Berücksichtigung der durch die Kugel gegebenen Bedingungen.
sol = FindMinimum[{potential, sphereconstr}, Thread[{vars, initpts}]];Extrahieren Sie die Gleichgewichtspositionen der Teilchen aus der Lösung.
solpts = Table[{x[i], y[i], z[i]}, {i, 1, n}] /. sol[[2]];Plotten Sie das Resultat.

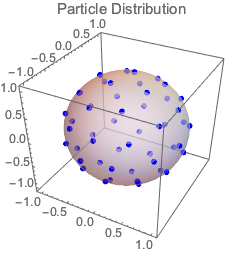
Show[ListPointPlot3D[solpts,
PlotRange -> {{-1.1, 1.1}, {-1.1, 1.1}, {-1.1, 1.1}},
PlotStyle -> {{PointSize[.03], Blue}}, AspectRatio -> 1,
BoxRatios -> 1, PlotLabel -> "Particle Distribution"],
Graphics3D[{Opacity[.5], Sphere[]}]]