Find the Largest Small Polygon: New in Wolfram Language 11

Find the Largest Small Polygon

Find the polygon with maximal area among polygons with sides and diameter .

In Mathematica 11, FindMinimum adds an IPOPT solver to solve large-scale constrained optimization problems more efficiently.

Denote by n the number of vertices of the polygon.

In[1]:=

n = 50;

Let be the polar coordinates of the vertex of the polygon.

In[2]:=

vars = Join[Array[r, n], Array[\[Theta], n]];

They satisfy the constraints , , , .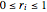

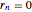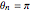In[3]:=

varbounds = 
  Join[Table[0 <= r[i] <= 1, {i, n - 1}], {r[n] == 0}, 
   Table[0 <= \[Theta][i] <= Pi, {i, n - 1}], {\[Theta][n] == Pi}];

The area of the polygon is the sum of the areas of triangles with vertices , , and (the origin).

In[4]:=

area = 1/2 Sum[
    r[i] r[i + 1] Sin[\[Theta][i + 1] - \[Theta][i]], {i, 1, n - 1}];

The distance between every two vertices should not exceed 1.

In[5]:=

constr1 = 
  Flatten[Table[
    0 < r[i]^2 + r[j]^2 - 
      2 r[i] r[j] Cos[\[Theta][i] - \[Theta][j]] <= 1, {i, 1, 
     n - 1}, {j, i + 1, n}], 2];

Due to the vertex ordering, the following constraints also exist.

In[6]:=

constr2 = Table[\[Theta][i] <= \[Theta][i + 1], {i, 1, n - 1}];

Choose initial points for the variables.

In[7]:=

x0 = vars /. {r[i_] -> 
     4. i (n + 1 - i)/(n + 1)^2, \[Theta][i_] -> \[Pi] i/n};

Maximize the area subject to the constraints.

In[8]:=

sol = FindMaximum[{area, constr1, constr2, varbounds}, 
   Thread[{vars, x0}]];

Convert to Cartesian coordinates.

In[9]:=

rectpts = 
  Table[FromPolarCoordinates[{r[i], \[Theta][i]}], {i, 1, n}] /. 
   sol[[2]];

Plot the solution.

In[10]:=

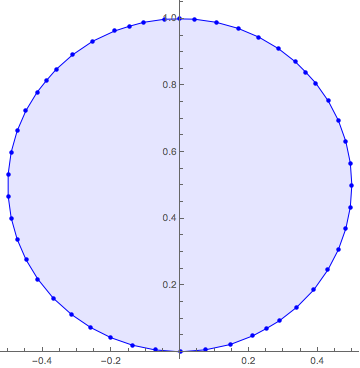
Show[ListPlot[rectpts, PlotStyle -> {Blue, PointSize -> Medium}], 
 Graphics[{Opacity[.1], Blue, EdgeForm[Blue], Polygon[rectpts]}], 
 AspectRatio -> 1, ImageSize -> Medium]

Out[10]=