Solve an ODE with a Ramp Forcing Function

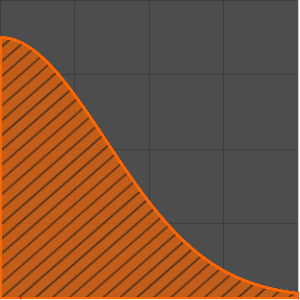
Compute a pure ramp response.

In[1]:=

sol = DSolveValue[{x''[t] + a^2 x[t] == Ramp[t - a], x[0] == 0, x'[0] == 0}, x[t], t, Assumptions -> a > 0] // FullSimplify

Out[1]=

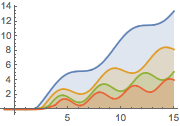
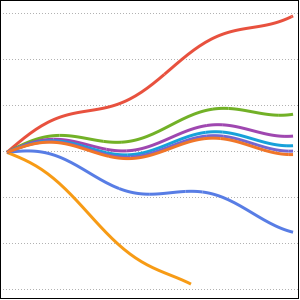
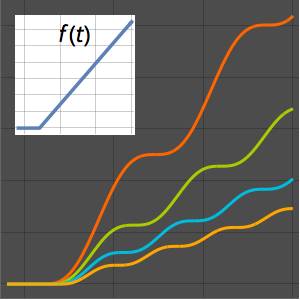
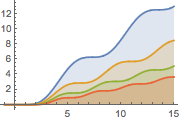
Plot the solution for different values of the parameter .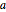

In[2]:=

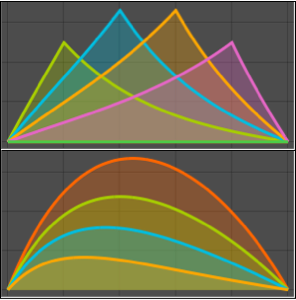
Plot[Table[sol, {a, 1, 2, 0.3}] // Evaluate, {t, -1, 15}, Filling -> Axis]

Out[2]=

Combine the ramp with an impulsive force.

In[3]:=

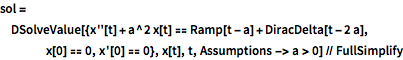
sol = DSolveValue[{x''[t] + a^2 x[t] == Ramp[t - a] + DiracDelta[t - 2 a], x[0] == 0, x'[0] == 0}, x[t], t, Assumptions -> a > 0] // FullSimplify

Out[3]=

In[4]:=

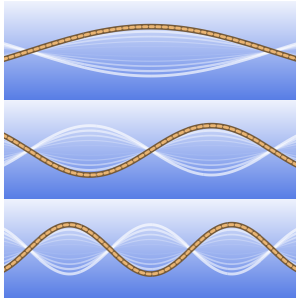
Plot[Table[sol, {a, 1, 2, 0.3}] // Evaluate, {t, -1, 15}, Filling -> Axis]

Out[4]=