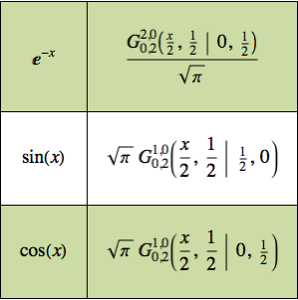Solve an Integro-Differential Equation

Solve an integro-differential equation.

In[1]:=

eqn = Derivative[1][y][x] == 1 + Sin[a x] + \!\( \*SubsuperscriptBox[\(\[Integral]\), \(0\), \(x\)]\(y[ t] \[DifferentialD]t\)\);

Obtain the general solution.

In[2]:=

sol1 = DSolveValue[eqn, y[x], x]

Out[2]=

Specify an initial condition to obtain a particular solution.

In[3]:=

init = y[0] == -1;

In[4]:=

sol2 = DSolveValue[{eqn, init}, y[x], x]

Out[4]=

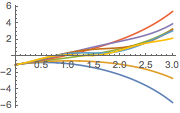
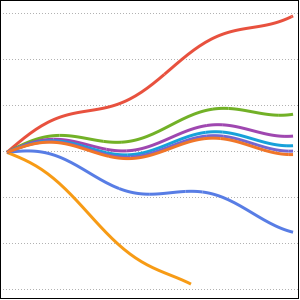
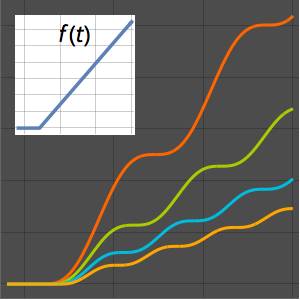
Plot the solution.

In[5]:=

Plot[Table[sol2, {a, -1, 4, 0.7}] // Evaluate, {x, 0, 3}]

Out[5]=