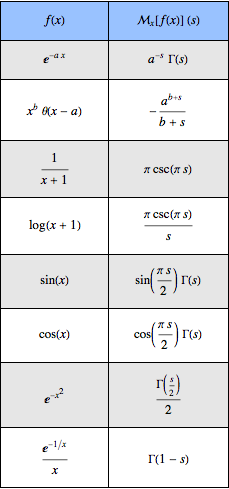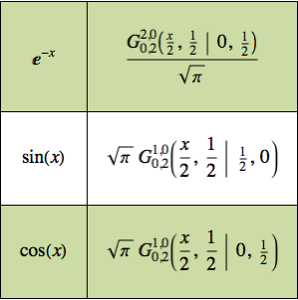Compute a Mellin Transform

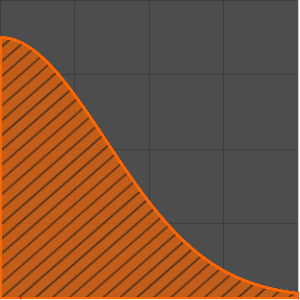
Compute the Mellin transform of a function using MellinTransform.

In[1]:=

MellinTransform[E^(-a x), x, s]

Out[1]=

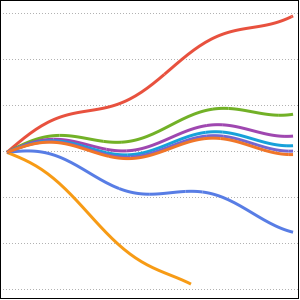
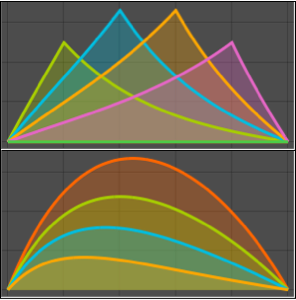
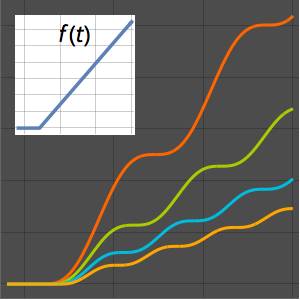
Plot the result for different values of .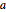

In[2]:=

MellinTransform[E^(-a x), x, s]; Plot[Table[% , {a, 1, 2, 1/4}] // Evaluate, {s, 0, 4}]

Out[2]=

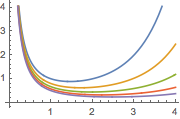
Generate conditions for the validity of the result.

In[3]:=

MellinTransform[E^(-a x), x, s, GenerateConditions -> True]

Out[3]=

Compute a multivariate Mellin transform.

In[4]:=

MellinTransform[Cos[x - y^2], {x, y}, {s, t}]

Out[4]=

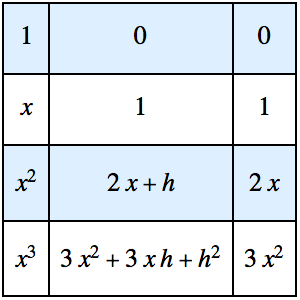
Create a table of basic Mellin transforms.

In[5]:=

flist = {E^(-a x), HeavisideTheta[x - a] x^b, 1/(1 + x), Log[1 + x], Sin[x], Cos[x], E^(-x^2), 1/(E^x^(-1) x)}; Grid[Map[Style[#, ScriptLevel -> 0] &, Join[{{HoldForm@f[x], HoldForm@MellinTransform[f[x], x, s]}}, Transpose[{flist, Map[MellinTransform[#, x, s] &, flist]}]], {2}], Dividers -> All, Spacings -> {4, 2}, Background -> {None, {{None, GrayLevel[.9]}}, {{1, 1} -> Hue[.6, .4, 1], {1, 2} -> Hue[.6, .4, 1]}}, BaseStyle -> {FontFamily -> Times, FontSize -> 13}] // TraditionalForm

Out[5]//TraditionalForm=