Optimal Truss Design
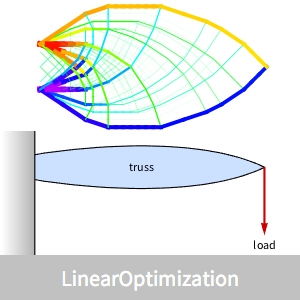
Design a minimum-weight truss that is anchored on one end to the wall and must withstand a load on the other end.
This example demonstrates how many features of the Wolfram Language may be used together to form a symbolic form of a linear optimization problem that can efficiently be solved by LinearOptimization.
Select a few specific positions where the truss is anchored to the wall.
The position where the load is applied is at the end of the truss.
The truss can be modeled using links and nodes. Each node is connected to a neighboring node by a link. One possible connectivity pattern is given here.
The candidate nodes are placed in a rectangular lattice.
Visualize the node positions, the anchor point positions, the position where force is applied and the connectivity of a single node in the middle of the truss.
Each node is associated with a unique index. Association efficiently provides a fast lookup table.
Find the indices associated with anchor and forcing points.
Construct a function that provides the connectivity of any lattice point for any given connectivity pattern.
For a given node 
, use the connectivity to determine which links include that node. If nodes 
and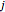 
are connected, then 
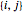and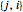 
represent the same link. To avoid repetition, consider only the one with 
.
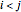Describe the set of links by ℒ such that if node 
and node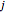 
form a link, then 
.
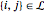Assume that the thickness of a link, and hence the mass per unit length, needs to be proportional to the force that will be exerted on that link. A convenient way to describe the links in ℒ is to have an indexing of links so that for each connected pair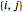 
, there is a unique index 
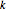with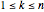 
.
The objective is to minimize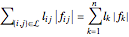 
, where 
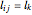is the length of the link between nodes 
and 
with index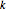 
and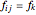 
is the force exerted by the link on its end joints.
The function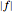 
is nonlinear, but can be expressed as a linear function by introducing 
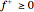and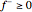 
such that 
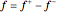and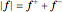 
. The objective is 
.
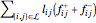At each node except the forcing point, there are no external forces applied.
At the forcing point, there is a vertical downward unit force applied.
At each non-anchoring node 
, there must be a force balance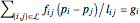 
, where 
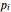is the position of the node 
and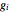 
is the external force at node 
. Define a function that gives the force balance constraint for node 
.
Use Complement to avoid including the anchor nodes.
The final constraints are:
Solve the resulting system.
Visualize the optimal truss with shades of blue indicating compression of links and shades of red indicating expansion of links.
