Correlated Measurements

Frequently, the analysis of measurements produces a collection of values whose uncertainties are correlated. When using those values in further computations, their correlations must be taken into account.

Here example H.3 of the document Guide to the Expression of Uncertainty in Measurement is followed. That example illustrates the process of linear calibration of a thermometer, using a least-squares fit.

Take a collection of pairs 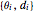, where 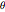is a temperature difference in degrees Celsius with respect to , and 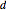is the deviation with the correct result.

Compute the best linear fit.

These are the parameters of the fit and their estimated uncertainties.

These are the covariance and correlation matrices of the fit. You can see the nonzero correlation between the values, expressed in the nonzero off-diagonal element of the correlation matrix.

They are related as follows.

To extrapolate the value of the temperature difference to 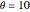degrees Celsius, with an estimation of uncertainty, it would be incorrect to perform either of these two computations, based on independent Around objects.

Those two equivalent computations ignore the correlation between the uncertainties of the parameters of the fit. To take them into account, the parameters are described using a VectorAround expression.