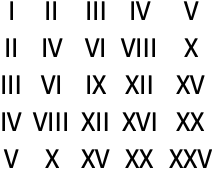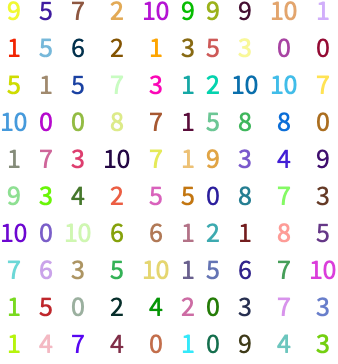| 13 | Arrays, or Lists of Lists |
We’ve seen how Table can be used to make lists. Now let’s see how Table can be used to create higher-dimensional arrays of values.
Make a list of 4 copies of x:
Table[x, 4]
Make a list of 4 copies of a list that contains 5 copies of x:
Table[x, 4, 5]
Use Grid to display the result in a grid:
Grid[Table[x, 4, 5]]
You can use Table with two variables to make a 2D array. The first variable corresponds to the row; the second to the column.
Make an array of colors: red going down, blue going across:
Grid[Table[RGBColor[r, 0, b], {r, 0, 1, .2}, {b, 0, 1, .2}]]
Show every array element as its row number:
Grid[Table[i, {i, 4}, {j, 5}]]
Grid[Table[j, {i, 4}, {j, 5}]]
Generate an array in which each element is the sum of its row and column number:
Grid[Table[i + j, {i, 5}, {j, 5}]]
Generate a multiplication table:
Grid[Table[i*j, {i, 5}, {j, 5}]]
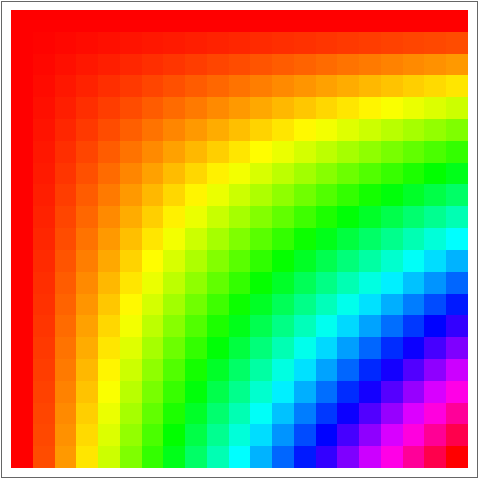
ArrayPlot lets you visualize values in an array. Larger values are shown darker.
Visualize a multiplication table:
ArrayPlot[Table[i*j, {i, 5}, {j, 5}]]
Generate and plot an array of random values:
ArrayPlot[Table[RandomInteger[10], 30, 30]]
ArrayPlot also lets you put colors as values:
ArrayPlot[Table[RandomColor[], 30, 30]]
Images are ultimately arrays of pixels. Color images make each pixel have red, green and blue values. Black-and-white images have pixels with values 0 (black) or 1 (white). You can get the actual pixel values using ImageData.
Find the value of pixels in an image of a “W”:
ImageData[Binarize[ Rasterize["W"] ]]
Use ArrayPlot to visualize the array of values:
ArrayPlot[ImageData[Binarize[ Rasterize["W"] ]]]
The image is of very low resolution, because that’s how Rasterize made it in this case. It’s also white-on-black instead of black-on-white. That’s because in an image 0 is black and 1 is white (like in RGBColor), while ArrayPlot’s default is to make larger values darker.
You can do arithmetic with arrays, just like lists. That means it’s easy to swap 0 and 1 in this array: Just subtract everything from 1, so every 0 becomes 1−0=1, and every 1 becomes 1−1=0.
Find pixel values, then do arithmetic to swap 0 and 1 in the array:
1 - ImageData[Binarize[ Rasterize["W"] ]]
The result is black-on-white:
ArrayPlot[1 - ImageData[Binarize[ Rasterize["W"] ]]]
| Table[x,4,5] | make a 2D array of values | |
| Grid[array] | lay out values from an array in a grid | |
| ArrayPlot[array] | visualize the values in an array | |
| ImageData[image] | get the array of pixel values from an image |
13.5Make a grid of all possible strings consisting of pairs of letters of the alphabet (“aa”, “ab”, etc.). »
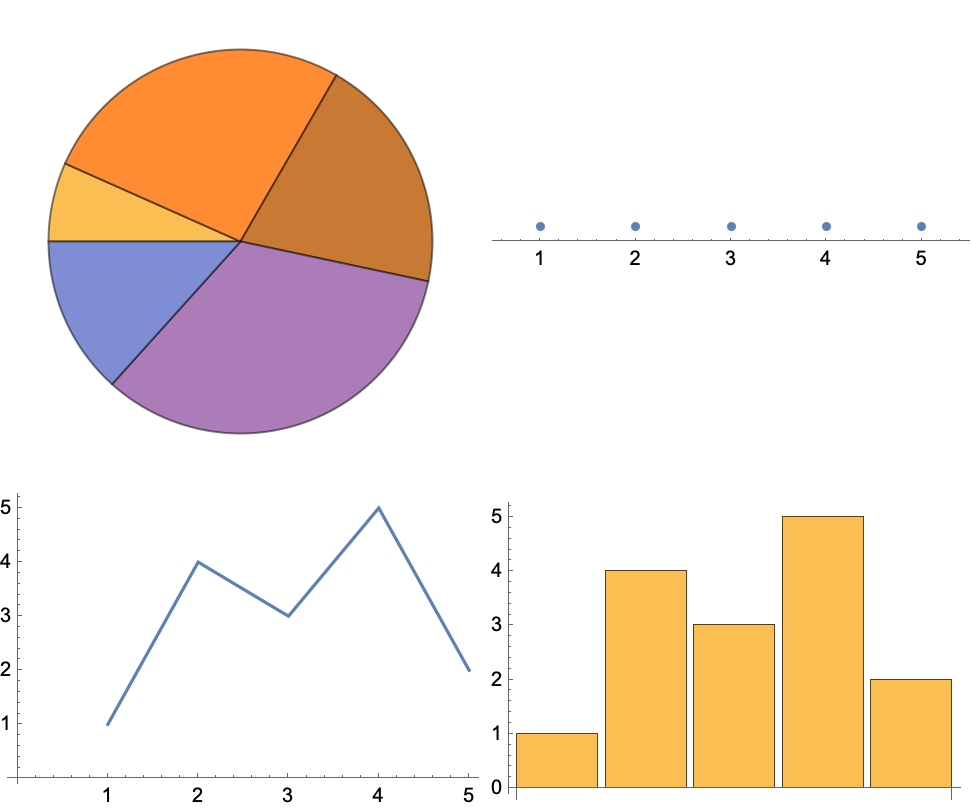
13.6Visualize {1, 4, 3, 5, 2} with a pie chart, number line, line plot and bar chart. Place these in a 2×2 grid. »
13.9Make an array plot of the lengths of Roman numeral strings in a multiplication table up to 100×100. »
+13.2Make a 10×10 grid of randomly colored random integers between 0 and 10 that have random size up to 32. »
Can the limits of one variable in a table depend on another?
Yes, later ones can depend on earlier ones. Table[x, {i, 4}, {j, i}] makes a “ragged” triangular array.
Can I make tables that are lists of lists of lists?
Yes, you can make tables of any dimension. Image3D gives a way to visualize 3D arrays.
Why does 0 correspond to black, and 1 to white, in images?
0 means zero intensity of light, i.e. black. 1 means maximum intensity, i.e. white.
How do I get the original image back from the output of ImageData?
Just apply the function Image to it.
- Arrays in the Wolfram Language are just lists in which each element is itself a list. The Wolfram Language also allows much more general structures, that mix lists and other things.
- Lists in the Wolfram Language correspond to mathematical vectors; lists of equal-length lists correspond to matrices.
- If most of the entries in an array are 0 (or some other fixed value), you can use SparseArray to construct an array just by giving the positions and values of nonzero elements.