| 27 | Applying Functions Repeatedly |
f[x] applies f to x. f[f[x]] applies f to f[x], or effectively nests the application of f. It’s common to want to repeat or nest a function.
This makes a list of the results of nesting f up to 4 times:
NestList[f, x, 4]
Using Framed as the function makes it a little more obvious what’s going on:
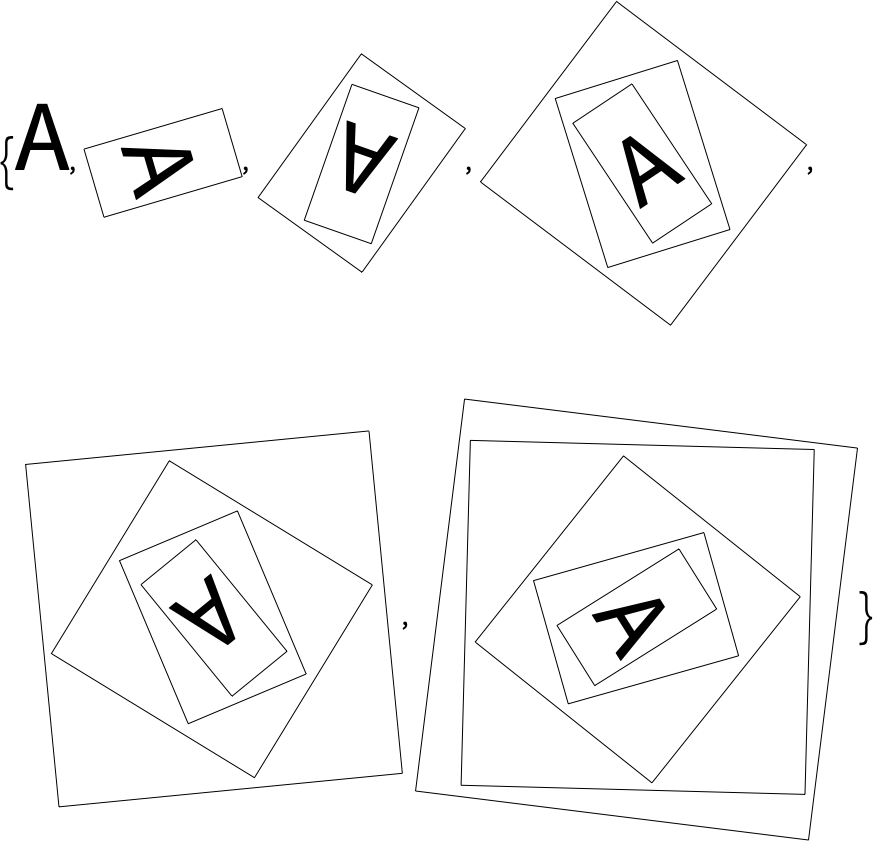
NestList[Framed, x, 5]
If you want to see a list of the results of successive nestings, use NestList. If you only want to see the final result, use Nest.
This gives the final result of 5 levels of nesting:
Nest[Framed, x, 5]
Nestedly apply EdgeDetect to an image, first finding edges, then edges of edges and so on.
Nestedly do edge detection on an image:
NestList[EdgeDetect, \!\(\*
GraphicsBox[RasterBox[CompressedData["
1:eJztmUFuwjAQRSP1JL1Ce5MegQv0CpEQEtyADUvEgiU3gAuwZ8meCyCYvmgk
y2oIDYkT/0W/flAUnPFXbI9nxu+T76/JW1EUn1wfXNW9/SML7vfMAm43O5/t
cLDt1pZLWyxsOrWyrH655wnP+Zc2tBwBdLTb2XxeaWhDWtKetwbC6WSrVVsx
dfIuFhLicrH1uruemNjBWn8cjzabpZHkxBo2O4OJypRIqCcmljsshOvVNpuh
JDmxTy8vfaWhJQVh7b/YcAP3cCjbgKk4miTnn5OfZZt2xbUhPT53F6n80quk
3ybge7NIcjZ5/j4bSn/Sex1soBklOeub+JjeoIm/vASurH1wMhzREDtVheEr
a4NI3JhdjxMlAQS02fU4URJApJ1djxMlAaQA2fU4URLgGYoCUeIgj8suJmbI
KwW/ley80lyDmv5qv8+vxxn7ds19UDNm0IyvRAbxYUFJMG431RzHJPNBU82d
TbLO4BCsyZhq/coka33hi6nVRQPUasgBgvX2ALWziRhq5zgx1M68niDd+eAP
mjcM6Q==
"], {{0, 0}, {80., 81.60000000000001}}, {0, 255},
ColorFunction->RGBColor],
ImageSize->{40.58203125, Automatic},
PlotRange->{{0, 80.}, {0, 81.60000000000001}}]\), 6]
Use a pure function to both edge-detect and color-negate at each step:
NestList[ColorNegate[EdgeDetect[#]] &, \!\(\*
GraphicsBox[RasterBox[CompressedData["
1:eJztmUFuwjAQRSP1JL1Ce5MegQv0CpEQEtyADUvEgiU3gAuwZ8meCyCYvmgk
y2oIDYkT/0W/flAUnPFXbI9nxu+T76/JW1EUn1wfXNW9/SML7vfMAm43O5/t
cLDt1pZLWyxsOrWyrH655wnP+Zc2tBwBdLTb2XxeaWhDWtKetwbC6WSrVVsx
dfIuFhLicrH1uruemNjBWn8cjzabpZHkxBo2O4OJypRIqCcmljsshOvVNpuh
JDmxTy8vfaWhJQVh7b/YcAP3cCjbgKk4miTnn5OfZZt2xbUhPT53F6n80quk
3ybge7NIcjZ5/j4bSn/Sex1soBklOeub+JjeoIm/vASurH1wMhzREDtVheEr
a4NI3JhdjxMlAQS02fU4URJApJ1djxMlAaQA2fU4URLgGYoCUeIgj8suJmbI
KwW/ley80lyDmv5qv8+vxxn7ds19UDNm0IyvRAbxYUFJMG431RzHJPNBU82d
TbLO4BCsyZhq/coka33hi6nVRQPUasgBgvX2ALWziRhq5zgx1M68niDd+eAP
mjcM6Q==
"], {{0, 0}, {80., 81.60000000000001}}, {0, 255},
ColorFunction->RGBColor],
ImageSize->{44.296875, Automatic},
PlotRange->{{0, 80.}, {0, 81.60000000000001}}]\), 6]
Add another yellow into the blend at each step:
NestList[Blend[{#, Yellow}] &, Red, 20]
If you successively apply a function that adds 1, you just get successive integers.
Nestedly add 1, getting successive numbers:
NestList[# + 1 &, 1, 15]
Nestedly multiply by 2, getting powers of 2.
The result doubles each time, giving a list of powers of 2:
NestList[2*# &, 1, 15]
Nested squaring very soon leads to big numbers:
NestList[#^2 &, 2, 6]
You can make nested square roots too.
Nestedly apply square root:
NestList[Sqrt[1 + #] &, 1, 5]
The decimal version of the result converges quickly (to the golden ratio):
NestList[Sqrt[1 + #] &, 1, 10] // N
RandomChoice randomly chooses from a list. You can use it to create a pure function that, say, randomly either adds +1 or −1.
Randomly add or subtract 1 at each step, starting from 0:
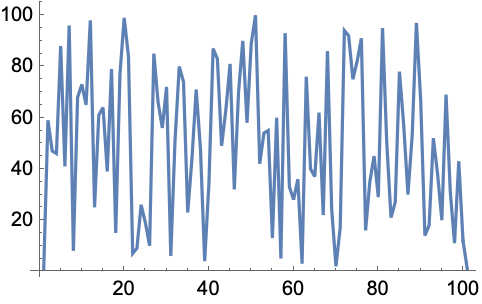
NestList[# + RandomChoice[{+1, -1}] &, 0, 20]
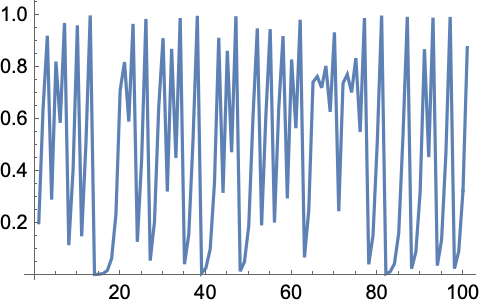
ListLinePlot[NestList[# + RandomChoice[{+1, -1}] &, 0, 500]]
So far, we’ve used NestList iteratively—effectively to perform a chain of applications of a particular function. But you can also use it for recursion, in which the very pattern of applications of the function is itself nested.
This does a chain of applications of the function f:
NestList[f[#] &, x, 3]
The pattern of applications of f is more complicated here:
NestList[f[#, #] &, x, 3]
Adding frames makes it a little easier to see what’s going on:
NestList[Framed[f[#, #]] &, x, 3]
Putting everything in columns shows the nested pattern of function applications.
The nested boxes are recursively combined in twos at each level:
NestList[Framed[Column[{#, #}]] &, x, 3]
NestList[Framed[Grid[{{#, #}, {#, #}}]] &, x, 3]
This forms the beginning of a fractal structure:
NestList[Framed[Grid[{{0, #}, {#, #}}]] &, x, 3]
It’s easy to get some pretty ornate recursive structures:
NestList[Flatten[{#, Rotate[#, 90 °], Rotate[#, 270 °]}] &, "R", 4]
Not all results from recursion are so complicated. Here’s an example that successively adds two shifted copies of a list together, as in {0,1,2,1}+{1,2,1,0}.
Prepend and append 0 to a list, then add together:
NestList[Join[{0}, #] + Join[#, {0}] &, {1}, 5]
If you put the result in a grid, it forms Pascal’s triangle of binomial coefficients:
NestList[Join[{0}, #] + Join[#, {0}] &, {1}, 8] // Grid
NestList is set up to recursively generate a list by repeatedly applying a function that gives a single result. But what if one has a function that gives multiple results? A list is no longer sufficient to represent what happens; instead one has to use a graph. And that’s where NestGraph comes in.
If one actually only has one result at each step, NestGraph produces a simple chain of results:
NestGraph[{f[#]}&, x, 5, VertexLabels->Automatic]
With two results at each step, however, it gives a tree:
NestGraph[{f[#],g[#]}&, x, 3, VertexLabels->Automatic]
There are two edges that come out of each node here, one representing the result of applying f, the other representing the result of applying g.
With the functions 2# and 2#+1, you still get a tree:
NestGraph[{2 #, 2 # + 1} &, 1, 3, VertexLabels -> All]
But with 2# and #+1, you don’t:
NestGraph[{2 #, # + 1} &, 1, 4, VertexLabels -> All]
With {2#, 2#+1}&, it works out that you’re always generating different numbers. But with {2#,#+1}&, you sometimes end up generating the same number in different ways. For example, 2#& applied to 2 gives 4. #+1& applied to 2 gives 3. But applying #+1& to 3 again gives 4. So this means there are two ways to get to 4, as represented by two “branches” merging at 4 in the graph generated by NestGraph.
Let’s say our function takes any country and gives a list of countries that border it. Starting from Switzerland, here’s the graph we get after one step, in effect showing the immediate neighbors of Switzerland.
One step in generating a graph of bordering countries around Switzerland:
NestGraph[#["BorderingCountries"] &,
Entity["Country", "Switzerland"], 1, VertexLabels -> All]
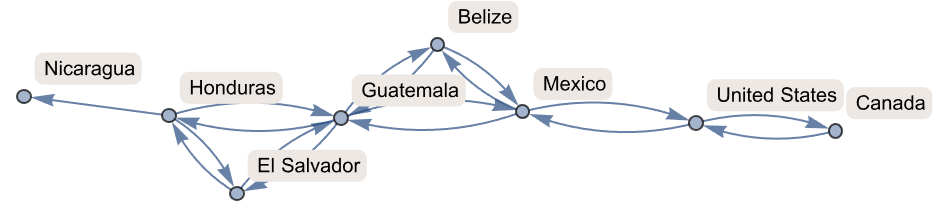
NestGraph[#["BorderingCountries"] &,
Entity["Country", "Switzerland"], 2, VertexLabels -> All]
The result of NestGraph is here showing us a network that includes not just immediate neighbors, but also neighbors of neighbors.
As another example, start from the word “hello” and successively connect every word to 3 words in the list of common words that Nearest considers nearest to it.
Create a network of nearby words with respect to 1-letter changes:
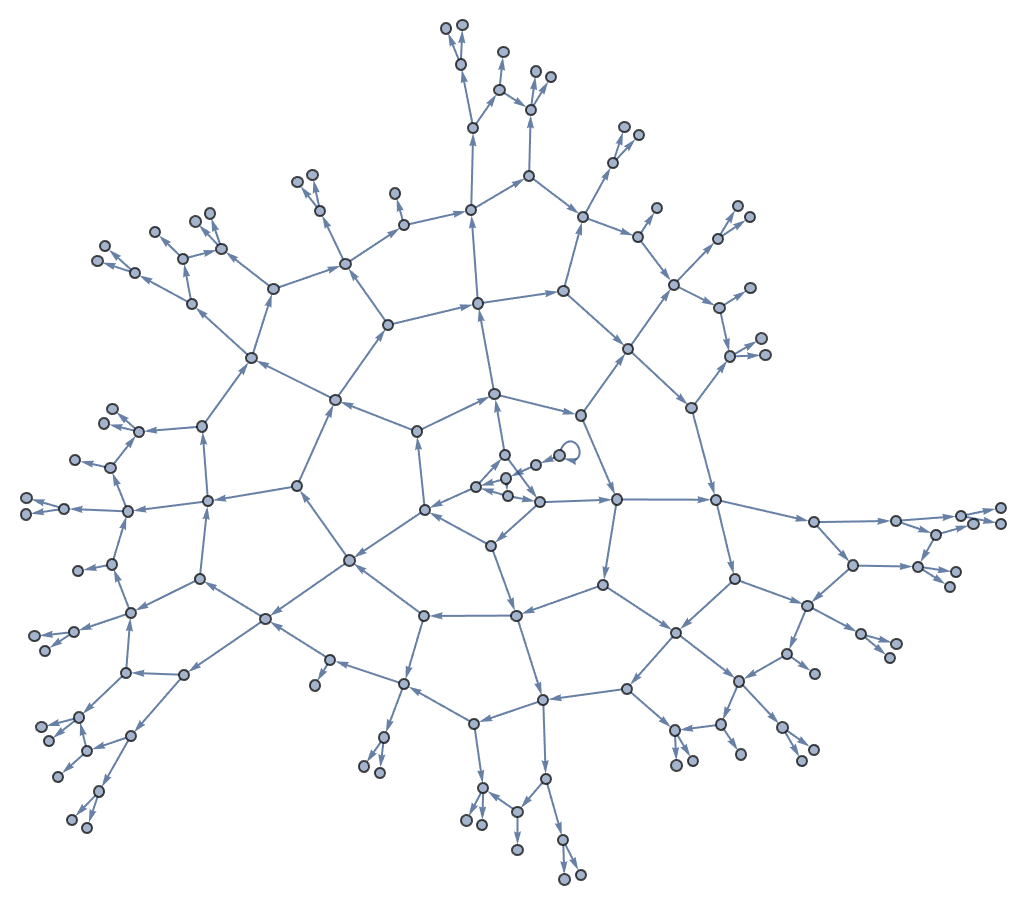
NestGraph[Nearest[WordList[], #, 3] &, "hello", 4,
VertexLabels -> All]
Within this graph, we can now find the shortest path from “hello” to “fallow”:
FindShortestPath[\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{"hello", "cello", "hallo", "cell", "hall", "hallow", "bell",
"call", "all", "ball", "allow", "callow", "ail", "alb",
"aglow", "allot", "bail", "belle", "fallow"}, {{{1, 2}, {1,
3}, {1, 1}, {2, 4}, {2, 2}, {2, 1}, {3, 5}, {3, 3}, {3, 6}, {
4, 7}, {4, 8}, {4, 4}, {5, 9}, {5, 10}, {5, 5}, {6, 11}, {6,
12}, {6, 6}, {9, 13}, {9, 14}, {9, 9}, {11, 15}, {11, 16}, {
11, 11}, {10, 9}, {10, 17}, {10, 10}, {7, 10}, {7, 7}, {7,
18}, {8, 9}, {8, 10}, {8, 8}, {12, 11}, {12, 12}, {12, 19}},
Null}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJw1V3k0FVrUv5cyz/e69xqLUNKopDTsLTJElMrcIA1EZEj0yhBFj2SIh0xR
FOmJSMm7EhnKPM9zdM3zdPHdb63vO/+ctdfZ56y9fmfv/fttmSuORtfYCASC
NpFA+N89K06nWN9fCNW4dBs7J3ogLc6wkLxIwpaan//2NhXCrX9Cfcyr+NCz
3NEIFeYg81e22JNCKhaFCkAHswXOfw6VTlYjI03Q7Z0q+woEivHvk/MhII9Z
sqjH7nkghocevr1fAvs82xS9VHtBpqtBzXaCioLWkV3GarPgV1PdLFBJRbvj
zJTLmUSMPSLxlfeoGMplbyvw3LUIV/sKT4o8GgXL+afLKqbTYJSyw6QlYhqO
RmyrevKKCW6GB1c9T4rjnqqslSRTTgx+y1SLj6WiZHAGnp/jwp4gmfU6h3pw
HItVfufWA4T/W59eX9nVWDsNpmcp3mmjklg4Knpd1m4FBN8yyn0OSuP/++lo
59fsNeqDNsVN3xxOsWN1kOAGnSgh3Gn7mOlg3QMvz7xUav4mhImXbo4EqnaC
r/4fq2NtQqg7bFcvL9oKF2QKol52C+GvRskOo8wGcDDwzv2nVgiPfbvAVnGx
BsQZ9lHKH4TwzbThWPifMgho49/P8BZCZeOjJhYPiuAmicvRXlMIfytdO2A3
mg9yxa9MzxOEUHziVvi46SdwPxJ1L81FEPfX/8f/OPoThH017ogcFUDlDvuo
E2+/gnPpkaEvdwTQqurgyCeR79DNmXNKniaA8wqNWz3TyuH9l/6shTZ+nLK2
1nhXWQMNMxDUXsSPH6/3bdkt3wj07LTdqbX86KCie4vs3woZLxWZhzgE8MBG
G42uuE7omHQxDbMUwI/mA8z+oB4oFlJvk6gSwKoMS9qt9l5w5f76creRILaV
+1nwveyDLR83yRR0CeLe4qTwrKo+GLJbPOS/XwgVl8vUBi/3gcCF2lR9FyG8
piB2ju1yLzyfv5l8eUYIAwvz3Q7F9gD3lsG/kgWEsUBovrPWpweGbYqTchSF
cTaLvXPOsgfOzdYK+WsK41jYD638nT3gzaU4yHlJGGPScrfcH+4GBXqcwzYP
YRzKEw1Bq25Iecyp0homjK85tAZIP7rAp8uWjfedMCot+xGMqF3wQbieYMFH
QkspfFc5XA/SYpcYa3IkzB3i4O5SqIdXMTpmHEdJ6Lq71GOfUR1wmduSrM+R
MCB0fFjPrhYO+mdocNqR8OYhM/5M5xq4Z6b5cNCbhM42dOXftVXgsfSsYzKC
hG0tl0qvxv0CSc6aDsk0Er6r1iVv162ACs2dvYQgEkZOELa7yBfBeVo213+3
SVj1nvpU+FkRuNXV96afJ+GkfG+Ij+x34NH+4dKmRkK+lMY/dt3foUvZMcFs
MwmDYh8WXC4phoP3l0UPcZBw1qt4oLm+BPI+hhgGjIqg+4D1kb08pdBpueuh
cb0I2q8OsufcKIMMxRJfDhdhfNyu2nTxShOg7KGYK+bCuEPYycNArhm+JBoq
WRwXRofyTK6lxWYw7t3ltLZdGM1vPInu6W4BhY8MNCcLoztd+s79llYY6D3L
dn9NCNM0abaH+tpgUJ3rze0/QujKVyZ9j9kOx/eXpWo2CiGf8Fn3fxQ6QXpA
M/crgYxu/ZFXjHILQfhNgLaNFhm3V12SKq37ChybTnrs9iNjfAtje1JQNjhy
J3jsyCGjaYVc32ezaFCNkeF50EhGo1N78y77J9M5jqQahfaR8cLzpLdj9/Lp
dSsL3ZfayRiSnqXQlf2DzrQ9/u+9QjI6hwYvbxWspse93/WC/TkZ++IcFDpF
6umPVt1EfczIWDPXld2R3Ug3jTd8ESnKej8zoUxVpZlueCM9JKWShHkiWdZW
7s30TQICS1f9SRh1LNSOw72J3ple+slah4QXb/LQPXQa6AG7K/xeipLwnPWO
L1RKLV3q++UguRkRfOWRUuKrUUF/903z+5t+EXzZ1KDmevcbXb/gpY3NsAjy
Hyg6TJ3LpN/O0ZJkJ5KQEHQiYSJRjP428PXDR0okTLQnRq7wZMD298HtIVdZ
+TXlefqy/2coFd1tk5DKyr+ilpujgoUw1iSz//IECRXvvnF7NFAIB580Xatf
5kWD0a1vR3PmoPSxzHpPMC+Gr2K4tfQ86HGfjJtS5kXdrQ7eV/LmIf62Wfzz
UR4kmP9Ui763AK11gtd4C3mwX//fXh2zRYgw+deNM5MH/baSvi9pLUF3Slyp
dwEPJla1deqpLMP10ntfU4Z4ULu24naj6ArYxbeUjirxooWI62a29hXgj4be
vY958bzoEZVBdyaUuXo6E6Z40f61u9r0IBNOWwR09l3jQ64WbAiRWAWNPSc8
Szv5kL9Buv0hZRX2/GZKOJzhx8mQ7yGUZiZc/3tCqeUzPx4WdByQsWICWVNA
IkdIAGP0zgqV5q9AP4euSPFpAVy6e2Erx9QyFAuX68m7CeCjUAt1Wf5lsHva
zR/pKYCvap4n9UstQbE3R3q4rQCmWpHMi/YuQnKoiK31QQEs9tI4xmGyABOt
hxrXxvgx9bN8w5+YeUgy8M4ZDOZHDhcl70quedDMcrEQk6Dh/Yf8iYSDLbCF
7Pst3oSGuxtD9ofubwaM1BaXC6ahX/M2iUitRhDLFrbemU9DL+zXe/m0Dt5s
cf/R2k5D82cVKn/ZV0FUT3S2yDgNDWK6J5TGf8BXHRrX+0kaHkj/KtKh8h9I
2DZK+fTTMKu600zmZwaEbP3iZ11KQ++dMWkKhfbgJz56WCaehlHPhOWjSl/T
nR+06F24SUPnIAG1pdxselCqYNL13TQ0pthIyLF/po+QSiaJU1QcVjaPTnT6
Qh/O8+PckU3FGOP0N2wjn+gdd+oiWjyo+CWgzC8u6gP9oIio7wcdKtLy1XU8
/RPo2e+TV9tkqUgu9XDaahsGXfkpooU8VDyZvfQxRjAbBgvSdowQqZjkYCf0
XecbFK4qfxvlomKBbJ/JduFyEE5OVzbaREWZQWZz054a6FOvJWdoUDFW/+3T
01b14BKSFZPmQsVRG3muhsFGcHjZPhb9k4SeEv0Xc8grUHLs3hmLEBJm+P3+
GXd4BeYt+EHHjIR2ni5cai9WYGRm09dcRRJG69T8Rd/JhK2vwTZgAwnfTMVR
DRhM8N3cVr86IoKKzNYFj5JVSM5vfBLeK4KZtFRP5oc1yF+6zTcyKIJh4L33
4ct1WKtt5/y2KIKXjpY7Fh8noNyLozemaCSc4zposPkNAVP1GBufaJJQo1R1
IXOZgNyKDiP97iTs0i6QcFMh4uvE6KNNWSQ8Gtl8o+ccETMLEm51jpNwUc8k
l8uEiIocea+NFcnYXVAZVnmYiM7xGkqfLpLxVYERNm4g4gE9Ob3vgWQkP3wl
75pDwHCrqPuFGWT0v66u5GFEQKhX/JBQRMZW4nHTH9/XYWBfqLpUORkDNzgt
czauwf3HngENrP5Y2jJsvnNoFSrVtFdOpJHR7MPiz3iuVQixn7SqfkzGio7m
m81aTAg8Vs9noUdE6o92L+lXc8BothPelUdEAy+G8dVDcxA7pbcrhMyGGvA2
yiN2FvLz319uMWfDMEudeytNM3Du/IJ+3mM2XG57Hcs+Nw1FNWNlXhFsWGWS
efzmhmn4vXBnozbr3O+X8/Yx0hQ8qHIoYpqxoeZYsbGO8iQMz81nmJDYsIlf
aziubRzI+KghPZeF43s+dvmkMTDTti1I0SViPec7Pr2qUXB68chyvo6AZQqV
HTz2o2BoKWrQY0ZAb4XhB7Y+o2CudOdZws91uPbLqojKPwaZ8Yl3i1bWQMeu
oPIxxzjsPamWOHh6Daylyg0dLk7ARdXXy96Nq2Dza49kl9ck5C9WjGwJXYXr
ekIxjjZTsBF6P635r4IPeUdruvk0xK4r1CR+WQVlfWWnfO0ZuNXJyT0pvwaJ
itmyNJlZ4Lb1PG72fQ22ymxMvd06y9Ifj/xVn6zD/lximMe1Oah4bU6tFZNA
8bLZsa06gyDfFs67RVQCqb3ftiwIDIGSr5EkSVoChyqbIKN2GNT/uZgjzdLn
B5b/cQ51Y0Du2bIidmMJrBF2j4wfHAF7dhuReh8JdC/ulerjHgPL7shIvhwJ
DN8jJ/W+bgzaBWHs+6gEaugcWAraPw5B96NFf8pLYrvVtvphxXG44xw30GMp
iZd09WQvZI/Bx1+OoT3Bkjjk1d6Q0TwKo+FyyRN5kvj6ao371eQRiL5ek5ja
IomZum1CYtsYsDmrQ/YQS59PBsRyO/01DPpRuiceT0ti1+Z7y305v2Fd68Gi
8ogkPuXQPHZmagAunD1+PK1JEl03WZc/0+4HNqayLC1XEi/OWdcxanrBZ/aX
s2mgJHqHlzV+T+qBmVuG39pNJdFgpdwhK7YbJgvl3vrKSGJ4aM/b5/QuqNF+
nu8+zMLvZHXDry9dEK351ZyZycIj42lpYnA3rP/u1CyrpuKI2A6X/qFp2Ouj
P/I4i4rmaWJNydzT0FIx6KceQEXAnyW/Dacg+P1KSsZZKj7ItGwL/zEJo1nl
bNtpVHyqyqPr7jYJdqJ24v6tFAwdjvLIvToJWsln08peUNB7JLrUKWwSPiQf
qei/QsET8vWN+cxJmK4zXnugTMEkWZWU4tgpUKXsuPKBn4IcnWB10mYaKvtG
ilrnRdHZvyRJ3WgGLjqqj96aEMVO94iH6XqzsHIoM2loQRS/7VJ+Gag5B5e4
4xvzBSmY3nnVZXzHPGgxaE+sVSh46vY0c3xuHqo6xQZdr1PwTOvavvSwBWAU
UqorEihY0bXPmrq0ALsuy/rldVJQ3kFvLUmWxYdHRwZOSFJx7c4d01d8ixD0
GCJvm1DRgap+3i9vAZQZf5XfCqTiitVW7VSlBZiv878z/JGFX8mxu2THeeD2
t2c/WEvFPSIfiX3Bc2CnctwxjZ+Kptpmsu67iRgYGpvX003BoHflthYSRPxy
RS1lPZOCsVNnSu+w7LtH0uMP+1LQWffRagnLf1Pg18R8UwoKNUTeN2H1S5sz
ZWZe+1jx3/6v71QIEadirohqi1LwafUL65VmIqakSb7xXBdF/NLBRVRiQ2rZ
3rM7ZkRxpL9F++4jNly9K+04MCmKFi2P2KX6WX3pbYJT0SILz7ia4r+BHU9Y
05Jv8FAwRTO78EYkO7oqM8LW5Sj4Ifr1zvh+dlQ5tkn0pDYFZXqMnYO2bMBq
TqkzaY4UHP4d3Lnn7AbUN6buUIul4D7FrpZTtzdg9Ccf+d4KCtbPGPT5eWzA
m5oaYbeWKMj73ojrhsMGvHNiiONfeSqaRNyRuWe4AWMCSrJCTlHR8wenj7L0
BiTuqXNQdqRisrqva28HOxJ4rhuts/LzlJCXZXQwO4b1yPxXGE3FeTHpD1yq
7DjLX2lps0JDT6uloQfRKxC7KFnjPEPDt+fS3frUmWCz9B/VdpaGC09vvFId
Y4LT7icuuEbDqqm+Krbnq9AeX/7nbyEx3H8Q+Zm71sBe5Rj5/nYx/C9X4eml
Tyy7/zDf9EkxTC0qUTq0dR0svQ1FHt4WQ+efC6spHutgUT1mHRAthtmLnD2C
6euwPngsWK1YDL8pW6XrfV6Htgh1p/xxMWSoVZ/OT14Hf/5XpD1UcTwbulRu
aLcOmdFhFxsOi6MSw/u5l8g6pAhWtApYiKM4j/4Opbg1OITXAh+6iCPDLDzP
SWgNXMVT90n7iSOTrab6rvMqmAQ/UtsWJI7uCQp1shUs/cieVq4VKI5Hzt9q
/SnNhOf+F/N8fVj37RZfjN1dAbf+51L6juKYK/+ruaZjGbb5NgTZnRdH5zXV
UbVzy6CPWvvYVcRx+bDXbtmBJeh6suPgA0FxxHNSBnahS1D4ufrwWgirzr0Z
F/9RmwYV3dMmf9tOwbYQ/SNEyjT4HSW2v9k3DY6SSRbihVNA/Um8pjswDQoG
zn6RR6fA7XxuVaHTDNRziGbEREyCw/SmtNOsoX7PmsnnD0kTEDjw4Ec4xyxI
uOjESy+MAYLvz/KNs6Cwd2NdP4xCGCOhdLV2Bna/MXHii2CAoZ9QxEaHGZjl
Dl+b4/8Dy+f2SJt3T8N5X/lZrsIhoNu3ZlTsnIadbEbFQQW/gal6x1PQegqe
uUllpZJ/g0/ZlUfqf0+C4BLbk6iqQSDkV3U9YPHiLg8+AZWJQRa/9Cdxfx2D
tv5O9Y+uv0HTwuu0gOYo/NVedbXUZAgoblZZm3lH4Fe870VC0DBol3xctpJl
QM/P5TEvAgM2GLt+ehb5B26G0sT6Ekfg87FOnTOOfyBcxJZhYTwGx5Y7En69
/wOLWv0ty1wT4Hfy4ZaAMwzomm7bde/0JMwGOUZ//DAFiiXWDo0ma5C1v32c
dGkKpE6TdVyV1yH1jw6vg8YUFOYpemjwE/CK2DHhK5enQEVzxP6gDwGXju46
cfTjFHgefzekN07AM8WrQWTWv912MpClGRDxqNstXQHGNHwrcc1ZiyFizl8R
+1s+z8CggcLC/RoiFvImWRyPm4WB+5SPjiNE7A3okJx/PAcaTtl6xxlE5M68
5HDMdh48IxLtOCqJaCp25n3jgQWwlNXicIkgYquKMeNd/wIkbed8XqFFxOxQ
6njitUUI734vkzZIwHId9XsiOYugkbTIU3yXgPa8XrmmlYsgMWfg9Dc7AQeu
CGzjzFgEPQ3F37Gb1kFq4oYIu/EimBIvvMzWYtVHFDvxRuUC/Og0Jog8WQXx
R2HyByQWgIfSdLZ5ignDRYbcA7qsOfBF2em+J0xwm6lN+MTSIYq0xF49EyaY
3oqfELk/C2v626N5LzDhfwAopY8S
"], {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium],
ArrowBox[BezierCurveBox[{1, 23, 26, 28, 34, 36, 39, 1},
SplineDegree->7], 0.055905301441446106`],
ArrowBox[
BezierCurveBox[{1, {4.62759957316787,
0.47186084003209017`}, 2}], 0.055905301441446106`],
ArrowBox[{1, 3}, 0.055905301441446106`],
ArrowBox[
BezierCurveBox[{2, {4.496795865781245,
0.18897740861252663`}, 1}], 0.055905301441446106`],
ArrowBox[BezierCurveBox[{2, 78, 81, 83, 89, 91, 94, 2},
SplineDegree->7], 0.055905301441446106`],
ArrowBox[{2, 4}, 0.055905301441446106`],
ArrowBox[
BezierCurveBox[{3, 101, 104, 106, 112, 114, 117, 3},
SplineDegree->7], 0.055905301441446106`],
ArrowBox[{3, 5}, 0.055905301441446106`],
ArrowBox[{3, 6}, 0.055905301441446106`],
ArrowBox[
BezierCurveBox[{4, 124, 127, 129, 135, 137, 140, 4},
SplineDegree->7], 0.055905301441446106`],
ArrowBox[{4, 7}, 0.055905301441446106`],
ArrowBox[{4, 8}, 0.055905301441446106`],
ArrowBox[
BezierCurveBox[{5, 147, 150, 152, 158, 160, 163, 5},
SplineDegree->7], 0.055905301441446106`],
ArrowBox[{5, 9}, 0.055905301441446106`],
ArrowBox[{5, 10}, 0.055905301441446106`],
ArrowBox[
BezierCurveBox[{6, 170, 173, 175, 181, 183, 186, 6},
SplineDegree->7], 0.055905301441446106`],
ArrowBox[{6, 11}, 0.055905301441446106`],
ArrowBox[{6, 12}, 0.055905301441446106`],
ArrowBox[
BezierCurveBox[{7, 193, 196, 198, 204, 206, 209, 7},
SplineDegree->7], 0.055905301441446106`],
ArrowBox[{7, 10}, 0.055905301441446106`],
ArrowBox[{7, 18}, 0.055905301441446106`],
ArrowBox[
BezierCurveBox[{8, 216, 219, 221, 227, 229, 232, 8},
SplineDegree->7], 0.055905301441446106`],
ArrowBox[{8, 9}, 0.055905301441446106`],
ArrowBox[{8, 10}, 0.055905301441446106`],
ArrowBox[
BezierCurveBox[{9, 239, 242, 244, 250, 252, 255, 9},
SplineDegree->7], 0.055905301441446106`],
ArrowBox[{9, 13}, 0.055905301441446106`],
ArrowBox[{9, 14}, 0.055905301441446106`],
ArrowBox[{10, 9}, 0.055905301441446106`],
ArrowBox[
BezierCurveBox[{10, 262, 265, 267, 273, 275, 278, 10},
SplineDegree->7], 0.055905301441446106`],
ArrowBox[{10, 17}, 0.055905301441446106`],
ArrowBox[
BezierCurveBox[{11, 285, 288, 290, 296, 298, 301, 11},
SplineDegree->7], 0.055905301441446106`],
ArrowBox[{11, 15}, 0.055905301441446106`],
ArrowBox[{11, 16}, 0.055905301441446106`],
ArrowBox[{12, 11}, 0.055905301441446106`],
ArrowBox[
BezierCurveBox[{12, 308, 311, 313, 319, 321, 324, 12},
SplineDegree->7], 0.055905301441446106`],
ArrowBox[{12, 19}, 0.055905301441446106`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}],
DiskBox[1, 0.055905301441446106],
DiskBox[2, 0.055905301441446106],
DiskBox[3, 0.055905301441446106],
DiskBox[4, 0.055905301441446106],
DiskBox[5, 0.055905301441446106],
DiskBox[6, 0.055905301441446106],
DiskBox[7, 0.055905301441446106],
DiskBox[8, 0.055905301441446106],
DiskBox[9, 0.055905301441446106],
DiskBox[10, 0.055905301441446106],
DiskBox[11, 0.055905301441446106],
DiskBox[12, 0.055905301441446106],
DiskBox[13, 0.055905301441446106],
DiskBox[14, 0.055905301441446106],
DiskBox[15, 0.055905301441446106],
DiskBox[16, 0.055905301441446106],
DiskBox[17, 0.055905301441446106],
DiskBox[18, 0.055905301441446106],
DiskBox[19, 0.055905301441446106]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics",
FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{232.7659912109375, Automatic}]\), "hello", "fallow"]
| NestList[ f,x,n] | make a list of applying f to x up to n times | |
| Nest [f,x,n] | give the result of applying f to x exactly n times | |
| NestGraph[ f,x,n] | make a graph by nestedly applying f starting with x |
27.1Make a list of the results of nesting Blur up to 10 times, starting with a rasterized size-30 “X”. »
27.2Start with x, then make a list by nestedly applying Framed up to 10 times, using a random background color each time. »
27.3Start with a size-50 “A”, then make a list of nestedly applying a frame and a random rotation 5 times. »
27.4Make a line plot of 100 iterations of the logistic map iteration 4 #(1-#)&, starting from 0.2. »
27.6Create a list of the first 10 powers of 3 (starting at 0) by nested multiplication. »
27.7Make a list of the result of nesting the (Newton’s method) function (#+2/#)/2& up to 5 times starting from 1.0, and then subtract 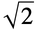 from all the results. »
from all the results. »
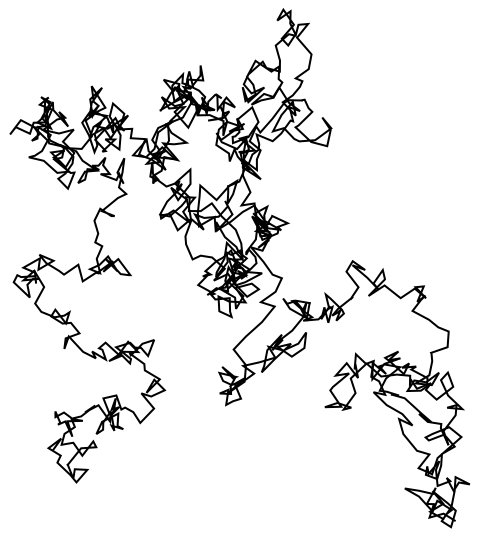
27.8Make graphics of a 1000-step 2D random walk which starts at {0, 0}, and in which at each step a pair of random numbers between −1 and +1 are added to the coordinates. »
27.9Make an array plot of 50 steps of Pascal’s triangle modulo 2 by starting from {1} and nestedly joining {0} at the beginning and at the end, and adding these results together modulo 2. »
27.10Generate a graph by starting from 0, then nestedly 10 times connecting each node with value n to ones with values n+1 and 2n. »
27.11Generate a graph obtained by nestedly finding bordering countries starting from the United States, and going 4 iterations. »
+27.1Make a line plot of 100 iterations of linear congruential function Mod[59#, 101]&, starting from 1. »
+27.4Generate a list of the numerical values obtained by up to 10 nestings of the function Sqrt[1+#]&. »
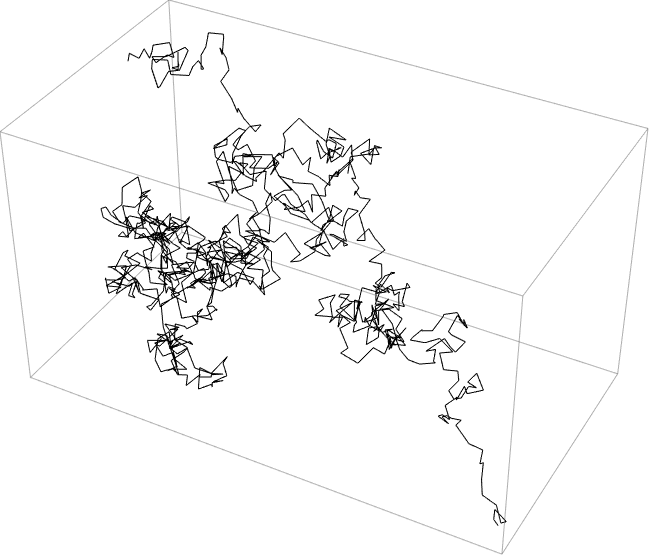
+27.5Make graphics of a 1000-step 3D random walk which starts at {0, 0, 0}, and in which at each step a triple of random numbers between −1 and +1 are added to the coordinates. »
What’s the difference between iteration and recursion?
If one does one thing repeatedly, it’s iteration. When one takes the result of an operation and applies the same operation to it wherever it is, that’s recursion. It’s slightly confusing, because simple cases of recursion are just iteration. NestList always does recursion, but if only one slot appears in the function, the recursion can be “unrolled” into iteration.
What is the relation between nesting, recursion and fractals?
They are very closely related. The definitions aren’t precise, but fractals are basically geometrical forms that exhibit some type of nested or recursive structure.
What is Pascal’s triangle?
It’s a very common structure discussed in elementary mathematics. Its definition is very close to the Wolfram Language code here: at each row each number is computed as the sum of the numbers directly above it and above it to its right. Each row gives the coefficients in the expansion of (1+x)^n.
Is NestGraph like a web crawler?
Conceptually yes. One can think of it as doing the analog of starting from a webpage and then visiting links from that page, and continuing recursively with that process. We’ll see an example of this in Section 44.
Why do some but not all countries have arrows both ways in the bordering countries graph?
If NestGraph was run for enough steps, all countries would have arrows both ways, since if A borders B, then B borders A. But here we’re stopping after just 2 steps, so many of the reverse connections haven’t been reached.
You don’t need to. You can just use Power, as in Table[2^n, {n, 0, 15}]. But it’s nice to see the sequence Plus, Times, Power arise from successive nesting (e.g. NestList[2+#&, 0, 15] is Table[2*n, {n, 0, 15}]).
Is there a way to keep applying a function until nothing is changing?
- NestList effectively traces out a “single path of computation”. NestGraph can be thought of as tracing out multiple “entangled” paths, to yield a multiway graph.
- NestGraph can be used, for example, to generate game graphs by having the results at each step correspond to possible moves in a game.
- Many examples of “nondeterministic computation” can be thought of as finding paths in graphs generated by NestGraph. Examples include theorem proving and parsing.
- The nearest words example can be made much more efficient by first computing a NearestFunction, then using this repeatedly, rather than computing Nearest from scratch for every word. This example is also closely related to NearestNeighborGraph, discussed in Section 22.