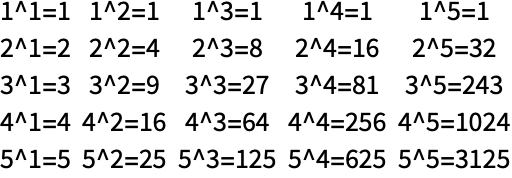| 42 | String Patterns and Templates |
String patterns work very much like other patterns in the Wolfram Language, except that they operate on sequences of characters in strings rather than parts of expressions. In a string pattern, you can combine pattern constructs like _ with strings like "abc" using ~~.
This picks out all instances of + followed by a single character:
In[1]:=
Out[1]=
This picks out three characters after each +:
In[2]:=
Out[2]=
Use the name x for the character after each +, and return that character framed:
In[3]:=
Out[3]=
In a string pattern, _ stands for any single character. __ (“double blank”) stands for any sequence of one or more characters, and ___ (“triple blank”) stands for any sequence of zero or more characters. __ and ___ will normally grab as much of the string as they can.
Pick out the sequence of characters between [ and ]:
In[4]:=
Out[4]=
__ normally matches as long a sequence of characters as it can:
In[5]:=
Out[5]=
Shortest forces the shortest match:
In[6]:=
Out[6]=
StringCases picks out cases of a particular pattern in a string. StringReplace makes replacements.
Make replacements for characters in the string:
In[7]:=
Out[7]=
Make replacements for patterns, using to compute ToUpperCase in each case:
In[8]:=
Out[8]=
Use NestList to apply a string replacement repeatedly:
In[9]:=
Out[9]=
StringMatchQ tests whether a string matches a pattern.
Select common words that match the pattern of beginning with a and ending with b:
In[10]:=
Out[10]=
Pick out any sequence of A or B repeated:
In[11]:=
Out[11]=
In a string pattern, LetterCharacter stands for any letter character, DigitCharacter for any digit character and Whitespace for any sequence of “white” characters such as spaces.
In[12]:=
Out[12]=
Pick out sequences of digit characters “flanked” by whitespace:
In[13]:=
Out[13]=
It’s common in practice to want to go back and forth between strings and lists. You can split a string into a list of pieces using StringSplit.
Split a string into a list of pieces, by default breaking at spaces:
In[14]:=
Out[14]=
This uses a string pattern to decide where to split:
In[15]:=
Out[15]=
Within strings, there’s a special newline character which indicates where the string should break onto a new line. The newline character is represented within strings as \n.
Split at newlines:
In[16]:=

Out[16]=
StringJoin joins any list of strings together. In practice, though, one often wants to insert something between the strings before joining them. StringRiffle does this.
Join strings, riffling the string "---" in between them:
In[17]:=
Out[17]=
In assembling strings, one often wants to turn arbitrary Wolfram Language expressions into strings. One can do this using TextString.
TextString turns numbers and other Wolfram Language expressions into strings:
In[18]:=
Out[18]=
A more convenient way to create strings from expressions is to use string templates. String templates work like pure functions in that they have slots into which arguments can be inserted.
In a string template each `` is a slot for a successive argument:
In[19]:=
Out[19]=
Named slots pick elements from an association:
In[20]:=
Out[20]=
You can insert any expression within a string template by enclosing it with <*...*>. The value of the expression is computed when the template is applied.
In[21]:=
Out[21]=
Use slots in the template (` is the backquote character):
In[22]:=
Out[22]=
The expression in the template is evaluated when the template is applied:
In[23]:=
Out[23]=
| patt1~~patt2 | sequence of string patterns | |
| Shortest[patt] | shortest sequence that matches | |
| StringCases[string,patt] | cases within a string matching a pattern | |
| StringReplace[string,pattval] | replace a pattern within a string | |
| StringMatchQ[string,patt] | test whether a string matches a pattern | |
| LetterCharacter | pattern construct matching a letter | |
| DigitCharacter | pattern construct matching a digit | |
| Whitespace | pattern construct matching spaces, etc. | |
| \n | newline character | |
| StringSplit[string] | split a string into a list of pieces | |
| StringJoin[{string1,string2, ...}] | join strings together | |
| StringRiffle[{string1,string2, ...},m] | join strings, inserting m between them | |
| TextString[expr] | make a text string out of anything | |
| StringTemplate[string] | create a string template to apply | |
| `` | slot in a string template | |
| < *...*> | expression to evaluate in a string template |
42.2Get a sorted list of all sequences of 4 digits (representing possible dates) in the Wikipedia article on computers. »
42.3Extract “headings” in the Wikipedia article about computers, as indicated by strings starting and ending with "===". »
42.5Find names of integers below 50 that have an “i” somewhere before an “e”. »
42.6Make any 2-letter word uppercase in the first sentence from the Wikipedia article on computers. »
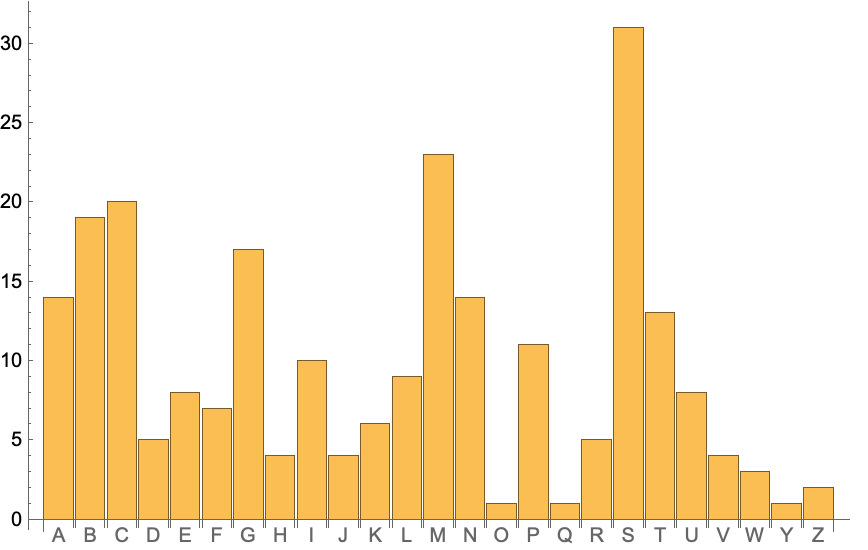
42.7Make a labeled bar chart of the number of countries whose TextString names start with each possible letter. »
42.8Find simpler code for
Grid[Table[StringJoin[TextString[i], "^", TextString[j], "=", TextString[i^j]], {i, 5}, {j, 5}]]. »
How should one read ~~ out loud?
It’s usually read “tilde tilde”. The underlying function is StringExpression.
How does one type `` to make a slot in a string template?
It’s a pair of what are usually called backquote or backtick characters. On many keyboards, they’re at the top left, along with ~ (tilde).
Can I write rules for understanding natural language?
Yes, but we didn’t cover that here. The key function is GrammarRules.
What does TextString do when things don’t have an obvious textual form?
It does its best to make something human readable, but if all else fails, it’ll fall back on InputForm.
- There’s a correspondence between patterns for strings, and patterns for sequences in lists. SequenceCases is the analog for lists of StringCases for strings.
- The option Overlaps specifies whether or not to allow overlaps in string matching. Different functions have different defaults.
- String patterns by default match longest sequences, so you need to specify Shortest if you want it. Expression patterns by default match shortest sequences.
- Among string pattern constructs are Whitespace, NumberString, WordBoundary, StartOfLine, EndOfLine, StartOfString and EndOfString.
- Anywhere in a Wolfram Language symbolic string pattern, you can use RegularExpression to include regular expression syntaxes like x* and [abc][def].
- TextString tries to make a simple human-readable textual version of anything, dropping things like the details of graphics. ToString[InputForm[expr]] gives a complete version, suitable for subsequent input.
- You can compare strings using operations like SequenceAlignment. This is particularly useful in bioinformatics.
- FileTemplate, XMLTemplate and NotebookTemplate let you do the analog of StringTemplate for files, XML (and HTML) documents and notebooks.
- The Wolfram Language includes the function TextSearch, for searching text in large collections of files.