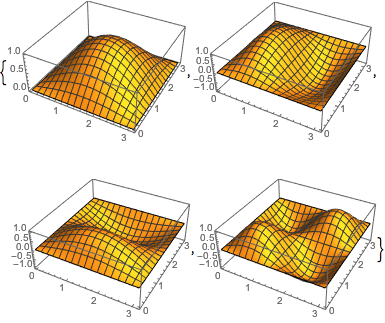
Calculate Exact Eigenfunctions for the Laplacian in a Rectangle

Specify a 2D Laplacian operator with homogeneous Dirichlet boundary conditions.

In[1]:=

{\[ScriptCapitalL], \[ScriptCapitalB]} = {-Laplacian[u[x, y], {x, y}], DirichletCondition[u[x, y] == 0, True]};

Find the four smallest eigenvalues and eigenfunctions in a rectangle.

In[2]:=

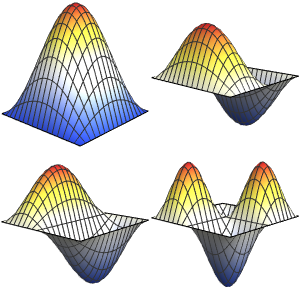
{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x, y], {x, 0, \[Pi]}, {y, 0, \[Pi]}, 4];

The eigenfunctions are trigonometric.

In[3]:=

funs

Out[3]=

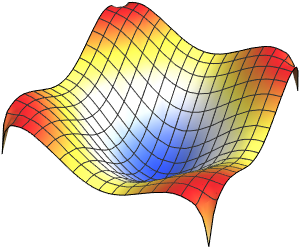
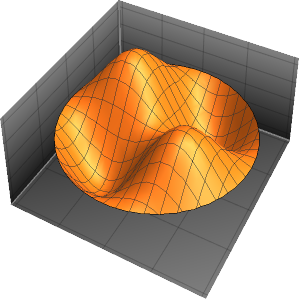
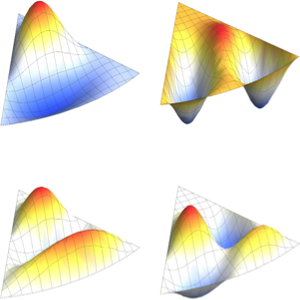
Visualize the eigenfunctions.

In[4]:=

Plot3D[#, {x, 0, \[Pi]}, {y, 0, \[Pi]}] & /@ funs

Out[4]=