Study a Sturm–Liouville System with Antiperiodic Boundary Conditions

Find the five smallest relational antiperiodic eigenvalues and eigenfunctions of a Sturm–Liouville operator.

Specify a Sturm–Liouville operator.

In[1]:=

V[x_] := Cos[x] + x; \[ScriptCapitalL] = -u''[x] - (V''[x] - V'[x]^2) u[x];

Specify a relational antiperiodic boundary condition.

In[2]:=

\[ScriptCapitalB] = PeriodicBoundaryCondition[-2 u[x], x == 2 \[Pi], TranslationTransform[{-2 \[Pi]}]];

Find the five smallest eigenvalues and eigenfunctions.

In[3]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, 2 \[Pi]}, 5];

Inspect the eigenvalues.

In[4]:=

vals

Out[4]=

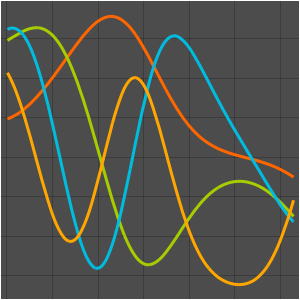
Visualize the eigenfunctions.

In[5]:=

Plot[funs, {x, 0, 2 \[Pi]}]

Out[5]=