Find the Spectrum of a Schrödinger Operator

Solve the eigenproblem of a Schrödinger equation 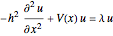over a 1D region.

Specify an unconstrained Schrödinger operator.

In[1]:=

h = 1/10; V[x_] := x^2 \[ScriptCapitalL] = -h^2*u''[x] + V[x]*u[x];

Find the 10 smallest eigenvalues and eigenfunctions on a refined mesh.

In[2]:=

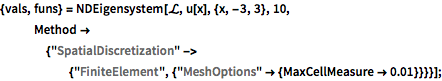
{vals, funs} = NDEigensystem[\[ScriptCapitalL], u[x], {x, -3, 3}, 10, Method -> {"SpatialDiscretization" -> {"FiniteElement", \ {"MeshOptions" -> {MaxCellMeasure -> 0.01}}}}];

Inspect the eigenvalues.

In[3]:=

vals

Out[3]=

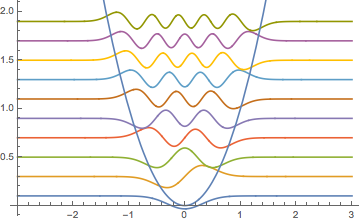
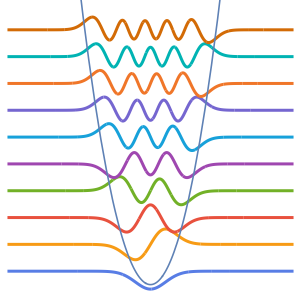
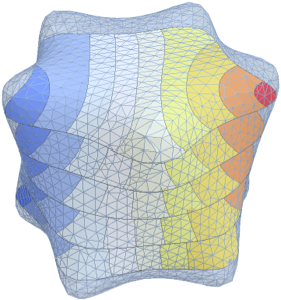
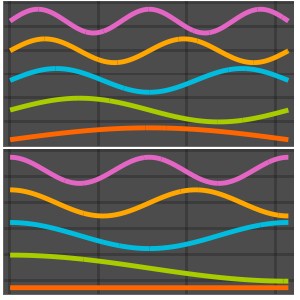
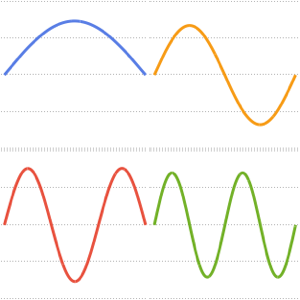
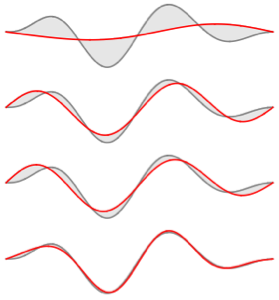
Visualize the eigenfunctions scaled by 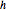and offset by the respective eigenvalues.

In[4]:=

Show[Plot[Evaluate[h*funs + vals], {x, -3, 3}], Plot[V[x], {x, -3, 3}], PlotRange -> {{-3, 3}, {0, 2}}, AxesOrigin -> {-3, 0}, ImageSize -> Medium]

Out[4]=