Random Vectors with Different Units

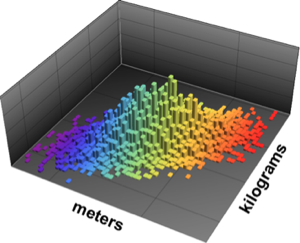
Define a joint height‐weight distribution with assumed correlation of 0.65.

In[1]:=

hw\[ScriptCapitalD] = BinormalDistribution[{Quantity[1.8, "Meters"], Quantity[85, "Kilograms"]}, {Quantity[0.15, "Meters"], Quantity[9, "Kilograms"]}, 0.65]

Out[1]=

Compute the probability of a person's height being over 1.75 meters, given that the person's weight is above 72 kilograms.

In[2]:=

NProbability[ h > Quantity[1.75, "m"] \[Conditioned] w > Quantity[72, "kg"], {h, w} \[Distributed] hw\[ScriptCapitalD]]

Out[2]=

Compute the distribution of the body mass index (BMI) for the assumed population.

In[3]:=

bmi\[ScriptCapitalD] = TransformedDistribution[ w/h^2, {h, w} \[Distributed] hw\[ScriptCapitalD]]

Out[3]=

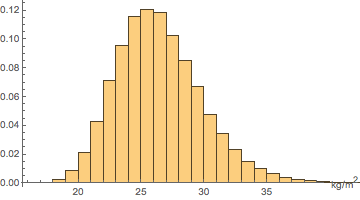
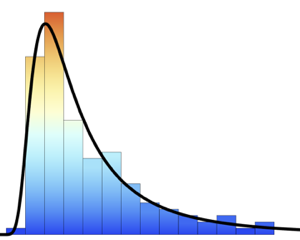
Estimate the distribution of the BMI using a sample histogram.

In[4]:=

sample = RandomVariate[bmi\[ScriptCapitalD], 10^5]; Histogram[sample, Automatic, "PDF", AxesLabel -> Automatic]

Out[4]=