Censored Distribution with Quantities

The body weight of adult males in the US is modeled with a normal distribution with mean of 191 lbs and standard deviation of 70 lbs. Assuming that bathroom scales have an upper limit of 300 lbs, find the distribution of weight as measured with a generic bathroom scale.

In[1]:=

\[ScriptCapitalD] = CensoredDistribution[{Quantity[0, "Pounds"], Quantity[300, "Pounds"]}, \[ScriptD] = NormalDistribution[Quantity[191, "Pounds"], Quantity[70, "Pounds"]]]

Out[1]=

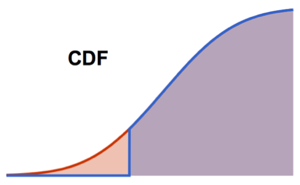
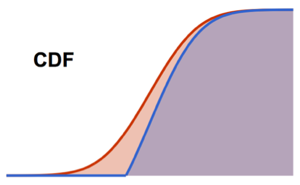
Cumulative distribution function.

In[2]:=

Plot[CDF[\[ScriptCapitalD], Quantity[x, "Pounds"]] // Evaluate, {x, 0, 350}, Filling -> Axis, Exclusions -> None, AxesLabel -> {"lb"}]

Out[2]=

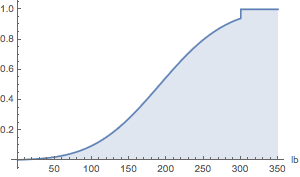
The average weight, assuming censoring is lower than that of the original distribution.

In[3]:=

{Mean[\[ScriptCapitalD]], Mean[\[ScriptD]]} // N

Out[3]=

The median weight according to the censored distribution is the same as that according to the original distribution.

In[4]:=

{Median[\[ScriptCapitalD]], Median[\[ScriptD]]}

Out[4]=