| 3 | First Look at Lists |
Lists are a basic way to collect things together in the Wolfram Language. {1, 2, 3} is a list of numbers. On their own, lists don’t do anything; they’re just a way to store things. So if you give a list as input, it’ll just come back unchanged:
In[1]:=
Out[1]=
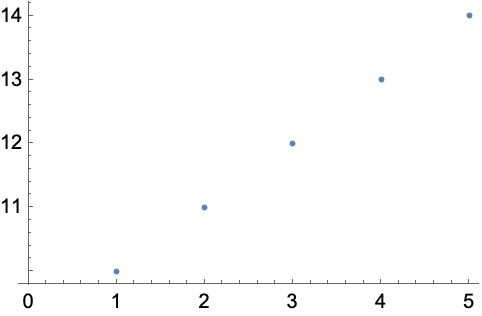
ListPlot is a function that makes a plot of a list of numbers.
Plot the list of numbers {1, 1, 2, 2, 3, 4, 4}:
In[2]:=
Out[2]=
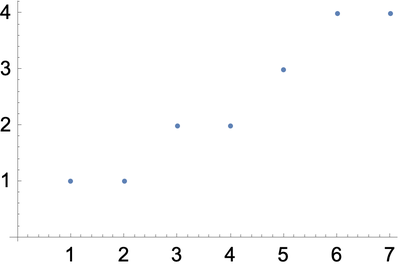
Plot the list of numbers {10, 9, 8, 7, 3, 2, 1}:
In[3]:=
Out[3]=
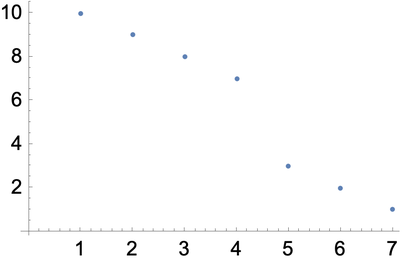
Range is a function that makes a list of numbers.
Generate a list of numbers up to 10:
In[4]:=
Out[4]=
In[5]:=
Out[5]=
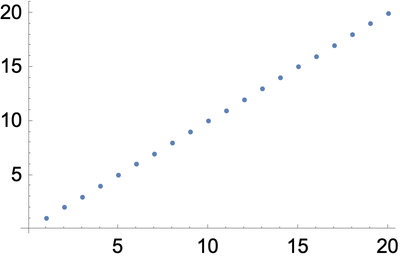
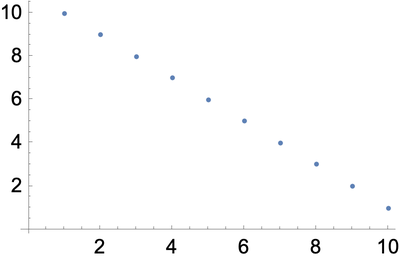
Reverse reverses the elements in a list.
Reverse the elements in a list:
In[6]:=
Out[6]=
Reverse what Range has generated:
In[7]:=
Out[7]=
Plot the reversed list:
In[8]:=
Out[8]=
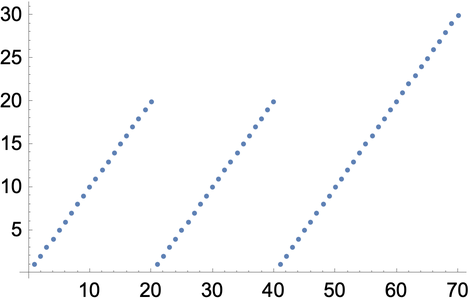
Join joins lists together, making a single list as the result.
Join lists together:
In[9]:=
Out[9]=
In[10]:=
Out[10]=
Join two lists made by Range:
In[11]:=
Out[11]=
In[12]:=
Out[12]=
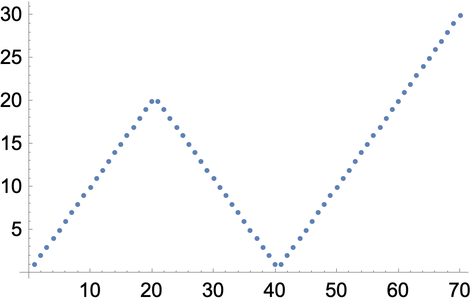
Reverse the list in the middle:
In[13]:=
Out[13]=
| {1,2,3,4} | list of elements | |
| ListPlot[{1,2,3,4}] | plot a list of numbers | |
| Range[10] | range of numbers | |
| Reverse[{1,2,3}] | reverse a list | |
| Join[{4,5,6},{2,3,2}] | join lists together |
3.2Make a list of numbers up to 100. »
3.4Make a list of numbers from 1 to 50 in reverse order. »
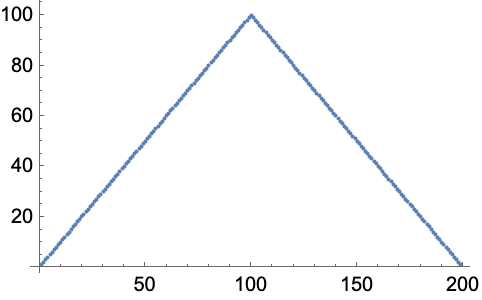
3.6Plot a list that counts up from 1 to 100, then down to 1. »
How does one read {1, 2, 3} out loud?
Usually “list 1 2 3”. “{” and “}” are called “braces” or “curly brackets”. “{” is “open brace” and “}” is “close brace”.
Is a list a function?
Yes. {1, 2, 3} is List[1, 2, 3]. But unlike, say, Plus, the function List doesn’t actually compute anything; it just comes back unchanged.
What is ListPlot plotting?
The values of successive list elements. The x value of each point gives the position in the list; the y value gives the value of that element.
How long can lists be?
As long as you want, until your computer runs out of memory.
- Range[m, n] generates numbers from m to n. Range[m, n, s] generates numbers from m to n in steps of s.
- Many computer languages have constructs like lists (often called “arrays”). But usually they only allow lists of explicit things, like numbers; you can’t have a list like {a, b, c} where you haven’t said what a, b and c are. You can in the Wolfram Language, though, because the Wolfram Language is symbolic.
- {a, b, c} is a list of elements in a definite order; {b, c, a} is a different list.
- Like in math, you can make theorems about Wolfram Language functions. For example, Reverse[Reverse[x]] is equal to x.