| 27 | Applying Functions Repeatedly |
f[x] applies f to x. f[f[x]] applies f to f[x], or effectively nests the application of f. It’s common to want to repeat or nest a function.
This makes a list of the results of nesting f up to 4 times:
In[1]:=
Out[1]=
Using Framed as the function makes it a little more obvious what’s going on:
In[2]:=
Out[2]=
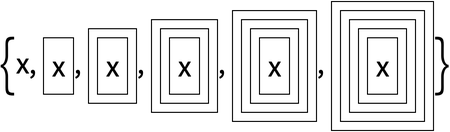
If you want to see a list of the results of successive nestings, use NestList. If you only want to see the final result, use Nest.
This gives the final result of 5 levels of nesting:
In[3]:=
Out[3]=

Nestedly apply EdgeDetect to an image, first finding edges, then edges of edges and so on.
Nestedly do edge detection on an image:
In[4]:=
Out[4]=

Use a pure function to both edge-detect and color-negate at each step:
In[5]:=
Out[5]=

Add another yellow into the blend at each step:
In[6]:=
Out[6]=
If you successively apply a function that adds 1, you just get successive integers.
Nestedly add 1, getting successive numbers:
In[7]:=
Out[7]=
Nestedly multiply by 2, getting powers of 2.
The result doubles each time, giving a list of powers of 2:
In[8]:=
Out[8]=
Nested squaring very soon leads to big numbers:
In[9]:=
Out[9]=
You can make nested square roots too.
Nestedly apply square root:
In[10]:=
Out[10]=
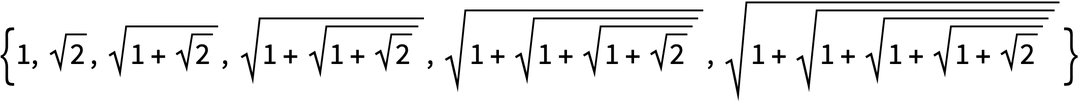
The decimal version of the result converges quickly (to the golden ratio):
In[11]:=
Out[11]=
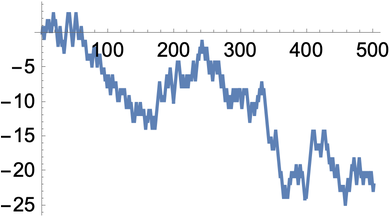
RandomChoice randomly chooses from a list. You can use it to create a pure function that, say, randomly either adds +1 or −1.
Randomly add or subtract 1 at each step, starting from 0:
In[12]:=
Out[12]=
In[13]:=
Out[13]=
So far, we’ve used NestList iteratively—effectively to perform a chain of applications of a particular function. But you can also use it for recursion, in which the very pattern of applications of the function is itself nested.
This does a chain of applications of the function f:
In[14]:=
Out[14]=
The pattern of applications of f is more complicated here:
In[15]:=
Out[15]=
Adding frames makes it a little easier to see what’s going on:
In[16]:=
Out[16]=
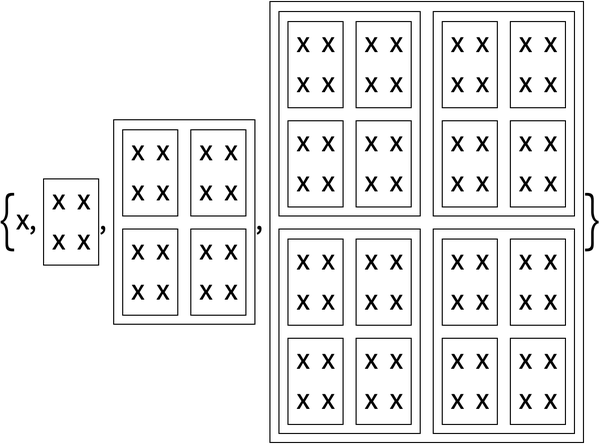
Putting everything in columns shows the nested pattern of function applications.
The nested boxes are recursively combined in twos at each level:
In[17]:=
Out[17]=
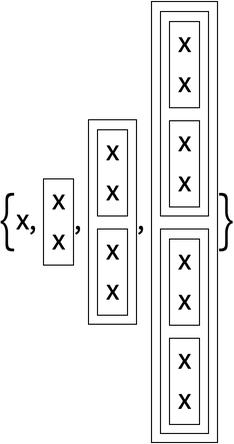
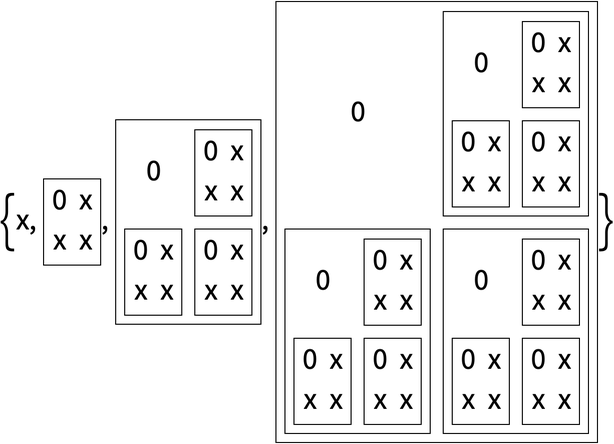
In[18]:=
Out[18]=
This forms the beginning of a fractal structure:
In[19]:=
Out[19]=
It’s easy to get some pretty ornate recursive structures:
In[20]:=
Out[20]=
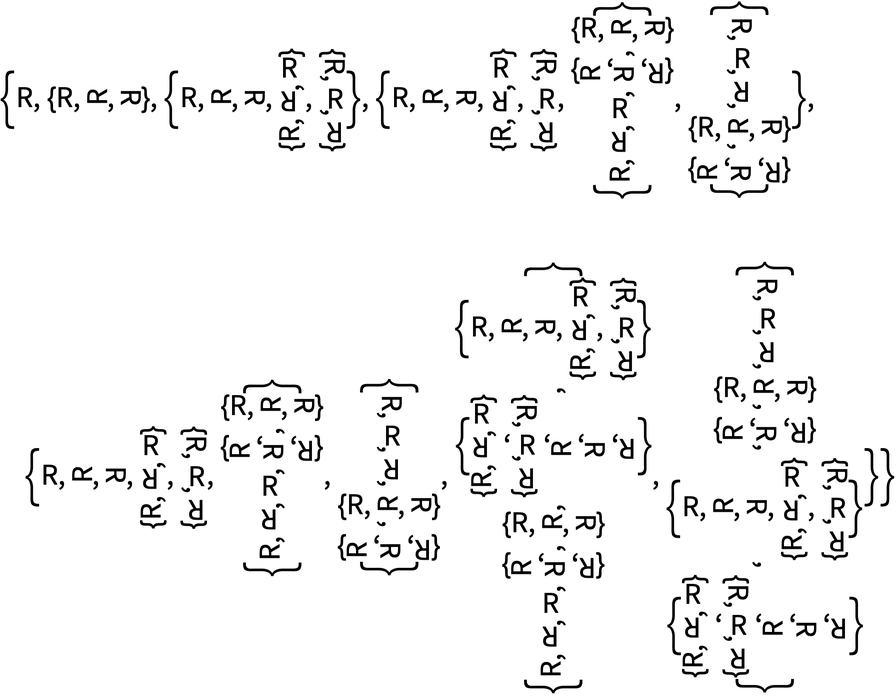
Not all results from recursion are so complicated. Here’s an example that successively adds two shifted copies of a list together, as in {0, 1, 2, 1}+{1, 2, 1, 0}.
Prepend and append 0 to a list, then add together:
In[21]:=
Out[21]=
If you put the result in a grid, it forms Pascal’s triangle of binomial coefficients:
In[22]:=
Out[22]=

NestList is set up to recursively generate a list by repeatedly applying a function that gives a single result. But what if one has a function that gives multiple results? A list is no longer sufficient to represent what happens; instead one has to use a graph. And that’s where NestGraph comes in.
If one actually only has one result at each step, NestGraph produces a simple chain of results:
In[155]:=
Out[155]=
With two results at each step, however, it gives a tree:
In[158]:=
Out[158]=
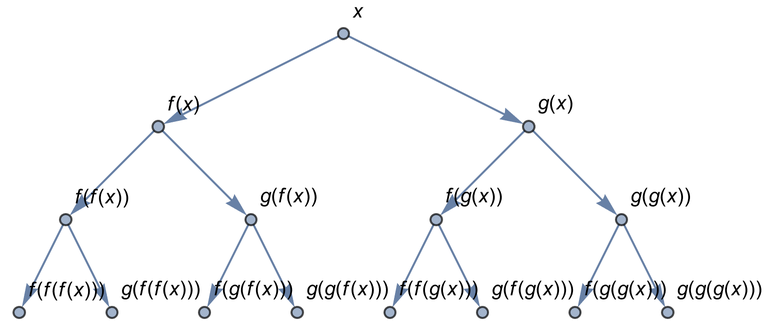
There are two edges that come out of each node here, one representing the result of applying f, the other representing the result of applying g.
With the functions 2# and 2#+1, you still get a tree:
In[164]:=
Out[164]=
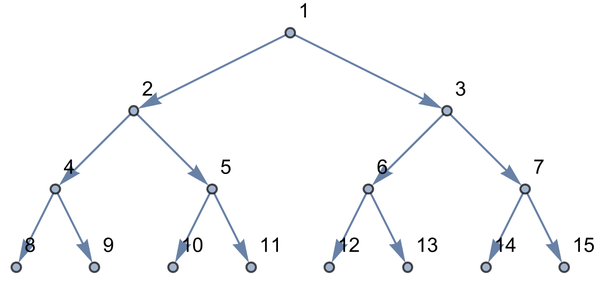
But with 2# and #+1, you don’t:
In[163]:=
Out[163]=
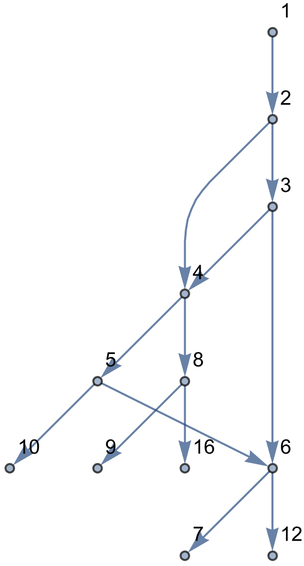
With {2#, 2#+1}&, it works out that you’re always generating different numbers. But with {2#, #+1}&, you sometimes end up generating the same number in different ways. For example, 2#& applied to 2 gives 4. #+1& applied to 2 gives 3. But applying #+1& to 3 again gives 4. So this means there are two ways to get to 4, as represented by two “branches” merging at 4 in the graph generated by NestGraph.
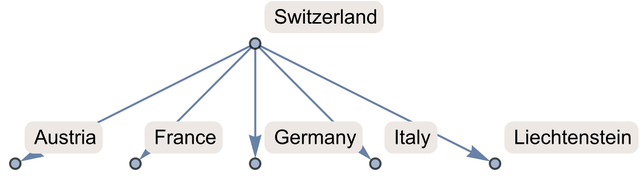
Let’s say our function takes any country and gives a list of countries that border it. Starting from Switzerland, here’s the graph we get after one step, in effect showing the immediate neighbors of Switzerland.
One step in generating a graph of bordering countries around Switzerland:
In[174]:=
Out[174]=
In[177]:=
Out[177]=
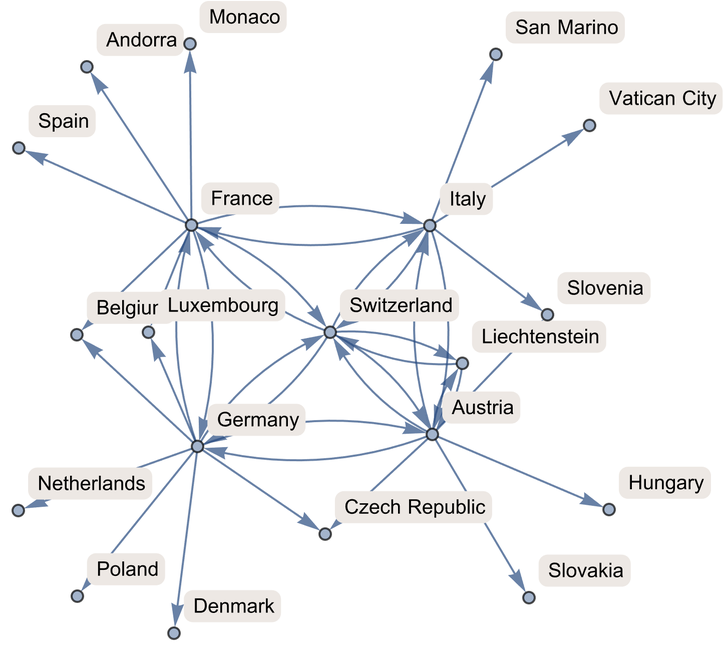
The result of NestGraph is here showing us a network that includes not just immediate neighbors, but also neighbors of neighbors.
As another example, start from the word “hello” and successively connect every word to 3 words in the list of common words that Nearest considers nearest to it.
Create a network of nearby words with respect to 1-letter changes:
In[28]:=
Out[28]=
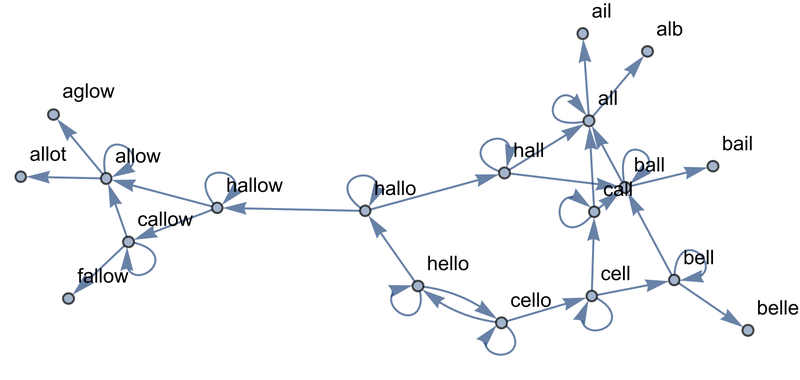
Within this graph, we can now find the shortest path from “hello” to “fallow”:
In[187]:=
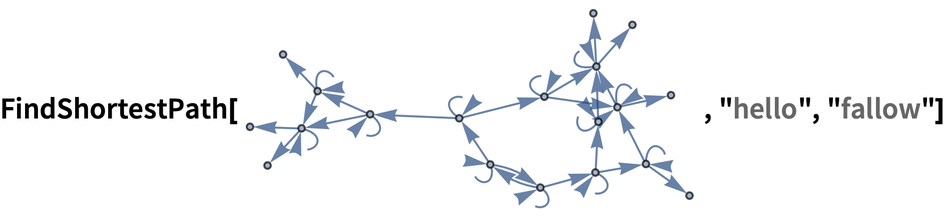
Out[187]=
| NestList[ f,x,n] | make a list of applying f to x up to n times | |
| Nest [f,x,n] | give the result of applying f to x exactly n times | |
| NestGraph[ f,x,n] | make a graph by nestedly applying f starting with x |
27.1Make a list of the results of nesting Blur up to 10 times, starting with a rasterized size-30 “X”. »
27.2Start with x, then make a list by nestedly applying Framed up to 10 times, using a random background color each time. »
27.3Start with a size-50 “A”, then make a list of nestedly applying a frame and a random rotation 5 times. »
27.4Make a line plot of 100 iterations of the logistic map iteration 4 #(1-#)&, starting from 0.2. »
27.6Create a list of the first 10 powers of 3 (starting at 0) by nested multiplication. »
27.7Make a list of the result of nesting the (Newton’s method) function (#+2/#)/2& up to 5 times starting from 1.0, and then subtract  from all the results. »
from all the results. »
27.8Make graphics of a 1000-step 2D random walk which starts at {0, 0}, and in which at each step a pair of random numbers between −1 and +1 are added to the coordinates. »
27.9Make an array plot of 50 steps of Pascal’s triangle modulo 2 by starting from {1} and nestedly joining {0} at the beginning and at the end, and adding these results together modulo 2. »
27.10Generate a graph by starting from 0, then nestedly 10 times connecting each node with value n to ones with values n+1 and 2n. »
27.11Generate a graph obtained by nestedly finding bordering countries starting from the United States, and going 4 iterations. »
+27.1Make a line plot of 100 iterations of linear congruential function Mod[59#, 101]&, starting from 1. »
+27.4Generate a list of the numerical values obtained by up to 10 nestings of the function Sqrt[1+#]&. »
+27.5Make graphics of a 1000-step 3D random walk which starts at {0, 0, 0}, and in which at each step a triple of random numbers between −1 and +1 are added to the coordinates. »
What’s the difference between iteration and recursion?
If one does one thing repeatedly, it’s iteration. When one takes the result of an operation and applies the same operation to it wherever it is, that’s recursion. It’s slightly confusing, because simple cases of recursion are just iteration. NestList always does recursion, but if only one slot appears in the function, the recursion can be “unrolled” into iteration.
What is the relation between nesting, recursion and fractals?
They are very closely related. The definitions aren’t precise, but fractals are basically geometrical forms that exhibit some type of nested or recursive structure.
What is Pascal’s triangle?
It’s a very common structure discussed in elementary mathematics. Its definition is very close to the Wolfram Language code here: at each row each number is computed as the sum of the numbers directly above it and above it to its right. Each row gives the coefficients in the expansion of (1+x)^n.
Is NestGraph like a web crawler?
Conceptually yes. One can think of it as doing the analog of starting from a webpage and then visiting links from that page, and continuing recursively with that process. We’ll see an example of this in Section 44.
Why do some but not all countries have arrows both ways in the bordering countries graph?
If NestGraph was run for enough steps, all countries would have arrows both ways, since if A borders B, then B borders A. But here we’re stopping after just 2 steps, so many of the reverse connections haven’t been reached.
You don’t need to. You can just use Power, as in Table[2^n, {n, 0, 15}]. But it’s nice to see the sequence Plus, Times, Power arise from successive nesting (e.g. NestList[2+#&, 0, 15] is Table[2*n, {n, 0, 15}]).
Is there a way to keep applying a function until nothing is changing?
- NestList effectively traces out a “single path of computation”. NestGraph can be thought of as tracing out multiple “entangled” paths, to yield a multiway graph.
- NestGraph can be used, for example, to generate game graphs by having the results at each step correspond to possible moves in a game.
- Many examples of “nondeterministic computation” can be thought of as finding paths in graphs generated by NestGraph. Examples include theorem proving and parsing.
- The nearest words example can be made much more efficient by first computing a NearestFunction, then using this repeatedly, rather than computing Nearest from scratch for every word. This example is also closely related to NearestNeighborGraph, discussed in Section 22.









