WOLFRAM

Stephen Wolfram
An Elementary Introduction to the Wolfram Language
Third Edition

30 Rearranging Lists

30Rearranging Lists
It’s common for lists that come out of one computation to have to be rearranged before going into another computation. For example, one might have a list of pairs, and need to convert it into a pair of lists, or vice versa.
Transpose a list of pairs so it becomes a pair of lists:
Transpose[{{1, 2}, {3, 4}, {5, 6}, {7, 8}, {9, 10}}]
 
Transpose the pair of lists back to a list of pairs:
Transpose[{{1, 3, 5, 7, 9}, {2, 4, 6, 8, 10}}]
 
Thread is a closely related operation, often useful for generating input to Graph.
“Thread” across the elements of two lists:
Thread[{1, 3, 5, 7, 9} -> {2, 4, 6, 8, 10}]
 
Partition takes a list, and partitions it into blocks of a specified size.
Partition a 12-element list into blocks of size 3:
Partition[Range[12], 3]
 
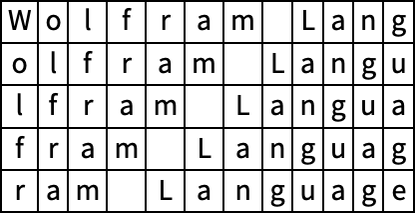
Partition a list of characters to display them in a grid:
Grid[Partition[ Characters["An array of text made in the Wolfram Language"], 9], Frame -> All]
 
If you don’t tell it otherwise, Partition breaks a list up into non-overlapping blocks. But you can also tell it to break the list into blocks that have some specified offset.
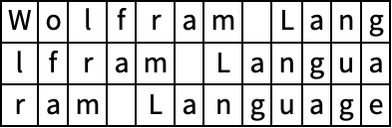
Partition a list into blocks of size 3 with offset 1:
Partition[Range[10], 3, 1]
 
Partition a list of characters into blocks with an offset of 1:
Grid[Partition[Characters["Wolfram Language"], 12, 1], Frame -> All]
 
Use an offset of 2 instead:
Grid[Partition[Characters["Wolfram Language"], 12, 2], Frame -> All]
 
Partition takes a list and breaks it into sublists. Flatten “flattens out” sublists.
Make a list of lists from digits of successive integers:
IntegerDigits /@ Range[20]
 
Make a flattened version:
Flatten[IntegerDigits /@ Range[20]]
 
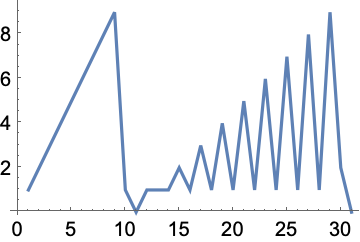
Make a plot from the sequence of digits:
ListLinePlot[Flatten[IntegerDigits /@ Range[20]]]
 
Flatten will normally flatten out all levels of lists. But quite often you only want to flatten, say, one level of lists. This makes a 4×4 table in which each element is itself a list.
Make a list of lists of lists:
Table[IntegerDigits[i^j], {i, 4}, {j, 4}]
 
Flatten everything out:
Flatten[Table[IntegerDigits[i^j], {i, 4}, {j, 4}]]
 
Flatten out only one level of list:
Flatten[Table[IntegerDigits[i^j], {i, 4}, {j, 4}], 1]
 
ArrayFlatten is a generalization of Flatten, which takes arrays of arrays, and flattens them into individual arrays.
This generates a deeply nested structure that’s hard to understand:
NestList[{{#, 0}, {#, #}} &, {{1}}, 2]
 
ArrayFlatten makes a structure that’s a little easier to understand:
NestList[ArrayFlatten[{{#, 0}, {#, #}}] &, {{1}}, 2]
 
With ArrayPlot, it’s considerably easier to see what’s going on:
ArrayPlot /@ NestList[ArrayFlatten[{{#, 0}, {#, #}}] &, {{1}}, 4]
 
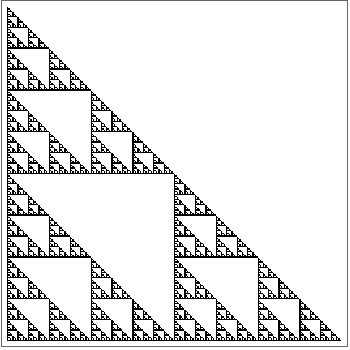
Generate a fractal Sierpinski pattern with 8 levels of nesting:
ArrayPlot[Nest[ArrayFlatten[{{#, 0}, {#, #}}] &, {{1}}, 8]]
 
There are many other ways to rearrange lists. For example, Split splits a list into runs of identical elements.
Split a list into sequences of successive identical elements:
Split[{1, 1, 1, 2, 2, 1, 1, 3, 1, 1, 1, 2}]
 
Gather, on the other hand, gathers identical elements together, wherever they appear.
Gather identical elements together in lists:
Gather[{1, 1, 1, 2, 2, 1, 1, 3, 1, 1, 1, 2}]
 
GatherBy gathers elements according to the result of applying a function to them. Here it’s using LetterQ, so that it gathers separately letters and non-letters.
Gather characters according to whether they are letters or not:
GatherBy[Characters["It's true that 2+2 is equal to 4!"], LetterQ]
 
SortBy sorts according to the result of applying a function.
Sort normally sorts shorter lists before longer ones:
Sort[Table[IntegerDigits[2^n], {n, 10}]]
 
Here SortBy is told to sort by the first element in each list:
SortBy[Table[IntegerDigits[2^n], {n, 10}], First]
 
Sort sorts a list in order. Union also removes any repeated elements.
Find all the distinct elements that appear:
Union[{1, 9, 5, 3, 1, 4, 3, 1, 3, 3, 5, 3, 9}]
 
You can use Union to find the “union” of elements that appear in any of several lists.
Get a list of all elements that appear in any of the lists:
Union[{2, 1, 3, 7, 9}, {4, 5, 1, 2, 3, 3}, {3, 1, 2, 8, 5}]
 
Find which elements are common to all the lists:
Intersection[{2, 1, 3, 7, 9}, {4, 5, 1, 2, 3, 3}, {3, 1, 2, 8}]
 
Find which elements are in the first list but not the second one:
Complement[{4, 5, 1, 2, 3, 3}, {3, 1, 2, 8}]
 
Find letters that appear in any of English, Swedish and Turkish:
Union[Alphabet["English"], Alphabet["Swedish"], Alphabet["Turkish"]]
 
Letters that appear in Swedish but not English:
Complement[Alphabet["Swedish"], Alphabet["English"]]
 
Another of the many functions you can apply to lists is Riffle, which inserts things between successive elements of a list.
Riffle x in between the elements of a list:
Riffle[{1, 2, 3, 4, 5}, x]
 
Riffle -- into a list of characters:
Riffle[Characters["WOLFRAM"], "--"]
 
Join everything together in a single string:
StringJoin[Riffle[Characters["WOLFRAM"], "--"]]
 
Functions like Partition let you take a list and break it into sublists. Sometimes you’ll instead just want to start from a collection of possible elements, and form lists from them.
Permutations gives all possible orderings, or permutations, of a list.
Generate a list of the 3!=3×2×1=6 possible orderings of 3 elements:
Permutations[{Red, Green, Blue}]
 
Generate all 23=8 possible subsets of a list of 3 elements:
Subsets[{Red, Green, Blue}]
 
Tuples takes a list of elements, and generates all possible combinations of a given number of those elements.
Generate a list of all possible triples of red and green:
Tuples[{Red, Green}, 3]
 
RandomChoice lets you make a random choice from a list of elements.
Make a single random choice from a list:
RandomChoice[{Red, Green, Blue}]
 
Make a list of 20 random choices:
RandomChoice[{Red, Green, Blue}, 20]
 
Make 5 lists of 3 random choices:
RandomChoice[{Red, Green, Blue}, {5, 3}]
 
RandomSample picks a random sample of elements from a list, never picking any particular element more than once.
Pick 20 elements from the range 1 to 100, never picking any number more than once:
RandomSample[Range[100], 20]
 
If you don’t say how many elements to pick you get a random ordering of the whole list:
RandomSample[Range[10]]
 
Vocabulary
Transpose[list] transpose inner and outer lists
Thread[list1list2] thread across elements of lists
Partition[list,n] partition into blocks of size n
Flatten[list] flatten out all sublists
Flatten[list,k] flatten out k levels of sublists
ArrayFlatten[list] flatten arrays of arrays
Split[list] split into runs of identical elements
Gather[list] gather identical elements into lists
GatherBy[list,f] gather according to results of applying f
SortBy[list,f] sort according to results of applying f
Riffle[list,x] riffle x between elements of list
Union[list] distinct elements in list
Union[list1,list2, ...] elements that appear in any of the lists
Intersection[list1,list2, ...] elements that appear in all the lists
Complement[list1,list2] elements that appear in list1 but not list2
Permutations[list] all possible permutations (orderings)
Subsets[list] all possible subsets
Tuples[list,n] all possible combinations of n elements
RandomChoice[list] random choice from list
RandomChoice[list,n] n random choices
RandomSample[list,n] n random non‐repeating samples
RandomSample[list] random ordering of a list
30.1Use Thread to make a list of rules with each letter of the alphabet going to its position in the alphabet. »
Expected output:
Out[]=
30.2Make a 4×6 grid of the first 24 letters of the alphabet. »
Expected output:
Out[]=
30.3Make a grid of the digits in 2^1000, with 50 digits per row, and put frames around everything. »
Expected output:
Out[]=
30.4Make a grid of the first 400 characters in the Wikipedia article for “computers”, with 20 characters per row, and frames around everything. »
Sample expected output:
Out[]=
30.5Make a line plot of the flattened list of the digits from the numbers from 0 to 200 (Champernowne sequence). »
Expected output:
Out[]=
30.6Make 4 steps in the “Menger sponge” analog of the fractal Sierpinski pattern from the text, but with a “kernel” of the form {{#, #, #}, {#, 0, #}, {#, #, #}}. »
Expected output:
Out[]=
30.7Find Pythagorean triples involving only integers by selecting {x, y, Sqrt[x^2+y^2]} with x and y up to 20. »
Expected output:
Out[]=
30.8Find the lengths of the longest sequences of identical digits in 2^n for n up to 100. »
Expected output:
Out[]=
30.9Take the names of integers up to 100 and gather them into sublists according to their first letters. »
Expected output:
Out[]=
30.10Sort the first 50 words in WordList[ ] by their last letters. »
Sample expected output:
Out[]=
30.11Make a list of the first 20 squares, sorted by their first digits. »
Expected output:
Out[]=
30.12Sort integers up to 20 by the length of their names in English. »
Expected output:
Out[]=
30.13Get a random sample of 20 words from WordList[ ], and gather them into sublists by length. »
Sample expected output:
Out[]=
30.14Find letters that appear in Ukrainian but not Russian. »
Expected output:
Out[]=
30.15Use Intersection to find numbers that appear both among the first 100 squares and cubes. »
Expected output:
Out[]=
30.16Find the list of countries that are in both NATO and the G8. »
Expected output:
Out[]=
30.17Make a grid in which all possible permutations of the numbers 1 through 4 appear as successive columns. »
Expected output:
Out[]=
30.18Make a list of all the different strings that can be obtained by permuting the characters in “hello”. »
Expected output:
Out[]=
30.19Make an array plot of the sequence of possible 5-tuples of 0 and 1. »
Expected output:
Out[]=
30.20Generate a list of 10 random sequences of 5 letters. »
Sample expected output:
Out[]=
30.21Find a simpler form for Flatten[Table[{i, j, k}, {i, 2}, {j, 2}, {k, 2}], 2]. »
Expected output:
Out[]=
+30.1Make an array plot from the numbers of the letters in the first 1000 characters in the Wikipedia article on “computers”, with 30 letters per row. »
Sample expected output:
Out[]=
+30.2Gather integers up to 30 into lists based on their values modulo 3. »
Expected output:
Out[]=
+30.3Gather the first 50 powers of 2 according to their last digits. »
Expected output:
Out[]=
+30.4Make a line plot of the result of sorting the numbers from −10 to +10 by their absolute values. »
Expected output:
Out[]=
+30.5Make a line plot of the list of the first 200 squares, sorted by their first digits. »
Expected output:
Out[]=
+30.6Make a line plot of integers up to 200 sorted by the lengths of their names in English. »
Expected output:
Out[]=
+30.7Get a random sample of 25 words from WordList[]. »
Sample expected output:
Out[]=
+30.8Riffle periods into the string “UNCLE” to make “U.N.C.L.E.”. »
Expected output:
Out[]=
+30.9Find letters that appear in Swedish or Polish but not English. »
Expected output:
Out[]=
+30.10Find countries that are in the World Health Organization but not the United Nations. »
Expected output:
Out[]=
+30.11Make a list of all pair-wise blends of red, green and blue. »
Expected output:
Out[]=
+30.12Make a list of array plots, each 50 rows high and with image size 50, of successive possible 8-tuples of 0 and 1. »
Expected output:
Out[]=
+30.13Generate 1000 random sequences of 4 letters, and make a list of ones that appear in WordList[ ].  »
Sample expected output:
Out[]=
Q&A
What does Partition do if the blocks don’t fit perfectly?
If it’s not told otherwise, it’ll only include complete blocks, so it’ll just drop elements that appear only in incomplete blocks. However, if you say for example Partition[list, UpTo[4]], it’ll make blocks up to length 4, with the last block being shorter if necessary.
Tech Note
  • Transpose can be thought of as transposing rows and columns in a matrix.
  • ArrayFlatten flattens an array of arrays into a single array, or alternatively, a matrix of matrices into a single matrix.
  • DeleteDuplicates[list] does the same as Union[list], except it doesn’t reorder elements.
More to Explore
Guide to Rearranging & Restructuring Lists in the Wolfram Language »
  • Download Notebook
  • Open in Wolfram Cloud
  • Discuss This Page
Next Section