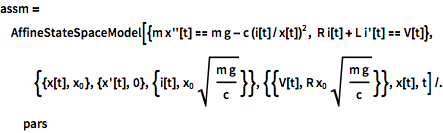Feedback Linearization 

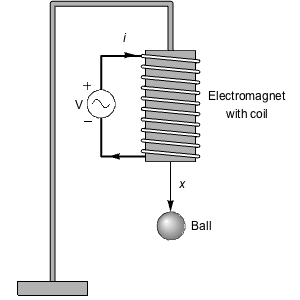
Feedback linearization is an exact linearization process that computes state and feedback transformations to linearize a nonlinear system and allows for the design of nonlinear controllers using linear techniques. Compare controller designs based on exact and approximate linearizations for a magnetically levitated system.

The affine model can be obtained directly from the governing equations.

In[1]:=

X pars = {R -> 10, L -> 0.05, m -> 0.05, g -> 9.8, c -> 0.05, Subscript[x, 0] -> 0.1};

In[2]:=

X assm = AffineStateSpaceModel[{m x''[t] == m g - c (i[t]/x[t])^2, R i[t] + L i'[t] == V[t]}, {{x[t], Subscript[x, 0]}, {x'[t], 0}, {i[t], Subscript[x, 0] Sqrt[(m g)/c]}}, {{V[t], R Subscript[x, 0] Sqrt[(m g)/c]}}, x[t], t] /. pars

Out[2]=

It is completely feedback linearizable, since there are no residual dynamics.

In[3]:=

X \[ScriptCapitalF] = FeedbackLinearize[ assm, {{Subscript[z, 1], Subscript[z, 2], Subscript[z, 3]}, v}];

In[4]:=

X \[ScriptCapitalF]["ResidualSystem"]

Out[4]=

Compute the stabilizing feedback gains using the exactly linearized system.

In[5]:=

X \[Kappa]1 = StateFeedbackGains[\[ScriptCapitalF][ "LinearSystem"], {-1.5, -2 + I, -2 - I}]

Out[5]=

Simulate the closed-loop system for given initial conditions.

In[6]:=

X csys1 = \[ScriptCapitalF][{"ClosedLoopSystem", \[Kappa]1}]; ics = {0.3, 0, 0.31305};

In[7]:=

X csys1 = \[ScriptCapitalF][{"ClosedLoopSystem", \[Kappa]1}]; ics = {0.3, 0, 0.31305};; or1 = OutputResponse[{csys1, ics}, 0, {t, 0, 35}]; Plot[%, {t, 0, 6}]

Out[7]=

Compute stabilizing feedback gains using the approximately linearized system.

In[8]:=

X \[Kappa]2 = StateFeedbackGains[assm, {-1.5, -2 + I, -2 - I}]

Out[8]=

The design based on exact linearization has a better response.

In[9]:=

X csys2 = SystemsModelStateFeedbackConnect[assm, \[Kappa]2]; or2 = OutputResponse[{csys2, ics}, 0, {t, 0, 35}];

In[10]:=

X Plot[{or1, or2}, {t, 0, 35}, PlotLegends -> {"Exact", "Approximate"}]

Out[10]=

The nonlinear controller used in the exact linearization design.

In[11]:=

X c1 = \[ScriptCapitalF][{"OriginalSystemFullController", \[Kappa]1}]

Out[11]=

The control effort expended.

In[12]:=

X inps1 = Join[{0}, sr1 = StateResponse[{csys1, ics}, 0, {t, 0, 35}]]; ce1 = OutputResponse[c1, inps1, {t, 0, 35}];

In[13]:=

X Plot[ce1, {t, 0, 35}, PlotRange -> All]

Out[13]=

The effort expended for the exact case is much lower than that of the approximate.

In[14]:=

X ce2 = -\[Kappa]2 /. Thread[{Subscript[\[FormalX], 1][t], Subscript[\[FormalX], 2][t], Subscript[\[FormalX], 3][t]} -> StateResponse[{csys2, ics}, 0, {t, 0, 35}]];

In[15]:=

X Plot[{ce1, ce2}, {t, 0, 35}, PlotLegends -> {"Exact", "Approximate"}]

Out[15]=

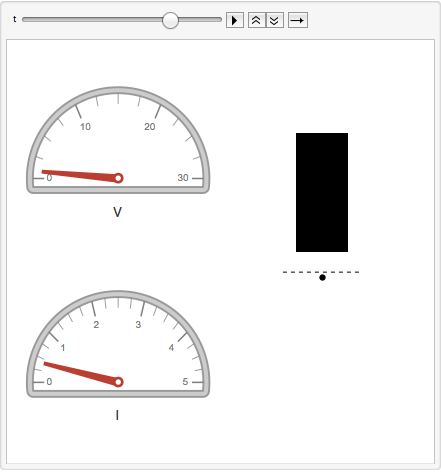
An animation of the ball being levitated using the nonlinear controller.

show complete Wolfram Language inputhide input

In[16]:=

X With[{v = ce1, x = sr1[[1]], i = sr1[[3]]}, Animate[GraphicsGrid[{{AngularGauge[v, {0, 30}, ScaleOrigin -> {\[Pi], 0}, GaugeLabels -> "V"], Graphics[{Rectangle[{-0.65, 0}, {0.65, 3}], Disk[{0, -5 x}, 0.08], Dashed, Line[{{-1, -0.5}, {1, -0.5}}]}, PlotRange -> {{-1, 1}, {-5, 5}}]}, {AngularGauge[i, {0, 5}, ScaleOrigin -> {\[Pi], 0}, GaugeLabels -> "I"], SpanFromAbove}}], {t, 0, 5}, SaveDefinitions -> True, AnimationRunning -> False]]

Play Animation Stop Animation