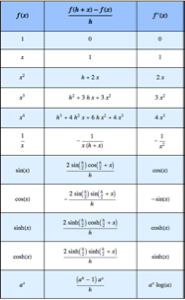
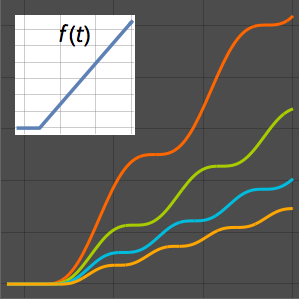
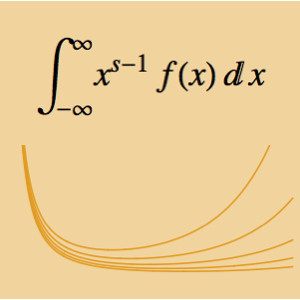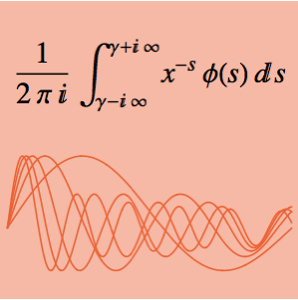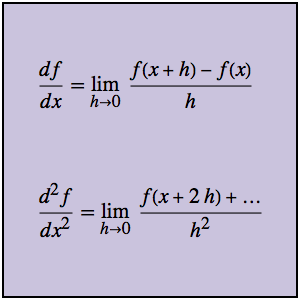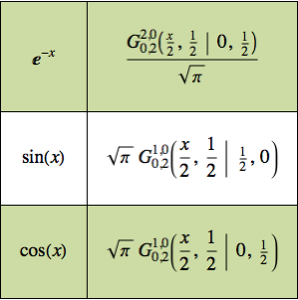Berechnen Sie definite Integrale mithilfe der G-Funktion: Neu in Wolfram Language 11

Berechnen Sie definite Integrale mithilfe der G-Funktion

Drückt man eine Funktion in einer MeijerG-Funktion aus, lässt sich so ihr Produkt über die positiven rellen Zahlen berechnen.

Legen Sie eine Regel fest, um das Integral eines Produkts von Funktionen in MeijerG-Funktionen auszudrücken.

In[1]:=

IntegrateMeijerG[f_ g_, {z_, 0, Infinity}] /; FreeQ[{f, g}, MeijerG] :=
  IntegrateMeijerG[
  MeijerGReduce[f, z] MeijerGReduce[g, z], {z, 0, Infinity}]

Dieses Integral kann ganz exakt in einem einzigen MeijerG-Ausdruck ausgedrückt werden.

In[2]:=

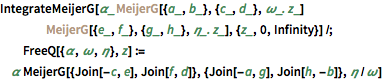
IntegrateMeijerG[\[Alpha]_ Inactive[MeijerG][{a_, b_}, {c_, 
      d_}, \[Omega]_. z_] Inactive[MeijerG][{e_, f_}, {g_, 
      h_}, \[Eta]_. z_], {z_, 0, Infinity}] /; 
  FreeQ[{\[Alpha], \[Omega], \[Eta]}, 
   z] := \[Alpha] MeijerG[{Join[-c, e], Join[f, d]}, {Join[-a, g], 
    Join[h, -b]}, \[Eta]/\[Omega]]

Werten Sie nach diesem Schema aus.

In[3]:=

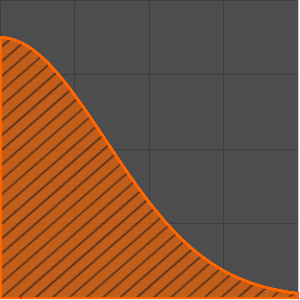
Plot[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, 10}, Filling -> Axis, 
 PlotRange -> All]

Out[3]=

In[4]:=

IntegrateMeijerG[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}]

Out[4]=

Mit Integrate erhalten Sie dasselbe Resultat.

In[5]:=

Integrate[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}]

Out[5]=

Obwohl die Antwort ziemlich anders aussieht, ist sie äquivalent.

In[6]:=

IntegrateMeijerG[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}];
Integrate[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}];
FullSimplify[% == %%]

Out[6]=