| 8 | Basic Graphics Objects |
In the Wolfram Language, Circle[] represents a circle. To display the circle as graphics, use the function Graphics. Later, we’ll see how to specify the position and size of a circle. But for now, we’re just going to deal with a basic circle, which doesn’t need any additional input.
Make graphics of a circle:
In[1]:=
Out[1]=

Disk represents a filled-in disk:
In[2]:=
Out[2]=

RegularPolygon gives a regular polygon with however many sides you specify.
Here’s a pentagon (5-sided regular polygon):
In[3]:=
Out[3]=

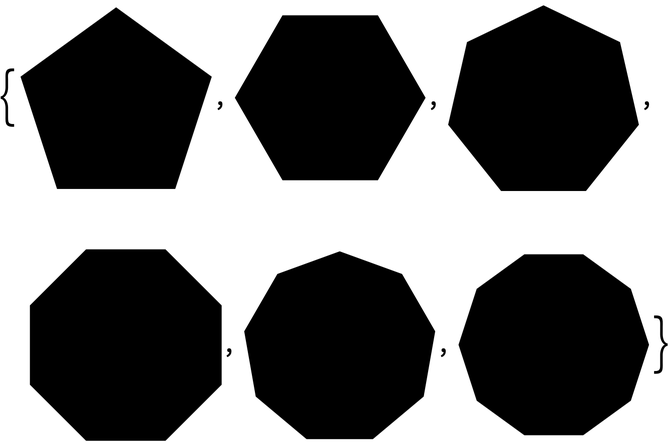
Make a table of graphics of regular polygons with between 5 and 10 sides:
In[4]:=
Out[4]=
Here’s an orange pentagon:
In[5]:=
Out[5]=

The Wolfram Language works in 3D as well as 2D, with constructs such as Sphere, Cylinder and Cone, as well as Cube, Tetrahedron, etc. When you have 3D graphics, you can rotate them around interactively to see different angles.
Display a sphere in 3D:
In[6]:=
Out[6]=

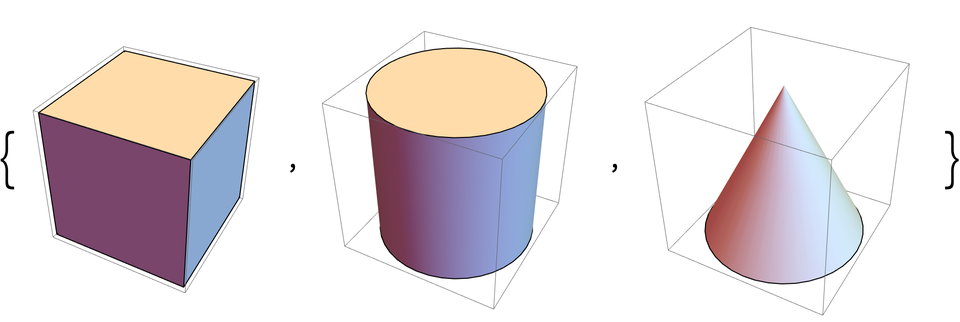
A list of a cube, a cylinder and a cone:
In[145]:=
Out[145]=
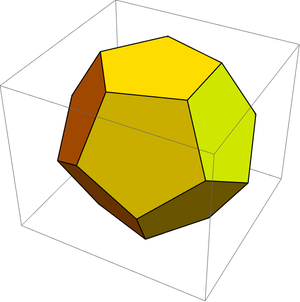
A yellow dodecahedron (polyhedron with 12 faces):
In[146]:=
Out[146]=
| Circle[ ] | specify a circle | |
| Disk[ ] | specify a filled‐in disk | |
| RegularPolygon[n] | specify a regular polygon with n sides | |
| Graphics[object] | display an object as graphics | |
| Sphere[ ], Cylinder[ ], Cone[ ], Cube[ ],... | specify 3D geometric shapes | |
| Graphics3D[object] | display an object as 3D graphics |
8.2Make graphics of a red circle. »
8.3Make a red octagon. »
8.4Make a list whose elements are disks with hues varying from 0 to 1 in steps of 0.1. »
8.5Make a column of a red and a green triangle. »
8.6Make a list giving the regular polygons with 5 through 10 sides, with each polygon being colored pink. »
8.7Make a graphic of a purple cylinder. »
8.8Make a list of polygons with 8, 7, 6, ..., 3 sides, and colored with RandomColor, then show them all overlaid with the triangle on top (hint: apply Graphics to the list). »
+8.1Make a list of 10 regular pentagons with random colors. »
+8.2Make a list of a 20-sided regular polygon and a disk. »
How can I make graphics with several objects?
Section 14 will explain. To do so requires understanding coordinates.
Why use Circle[], not just Circle?
For consistency. As we’ll see in Section 14, Circle[] is actually short for Circle[{0, 0}, 1], which means a circle of radius 1 and center coordinates {0, 0}.
Why isn’t the yellow dodecahedron pure yellow?
Because the Wolfram Language displays it like an actual 3D object, with lighting. If it were pure yellow, it would be hard to see its 3D structure.
What polyhedra can I use?
The platonic solids Tetrahedron[], Cube[], Octahedron[], Dodecahedron[], Icosahedron[], as well as UniformPolyhedron[{n, m}] (n-sided faces with m faces at each vertex), and in general any polyhedron.











