Mathematica 9の新機能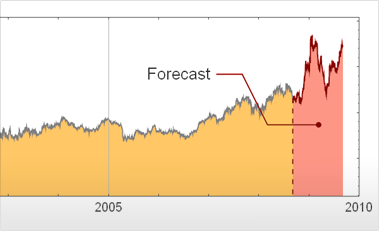
時系列と確率微分方程式
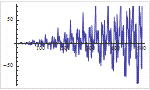
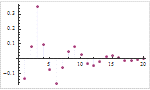
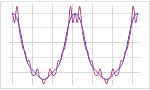
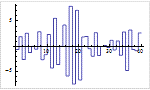
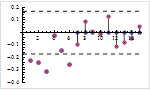
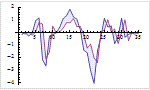
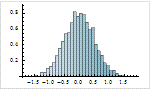
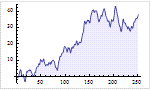
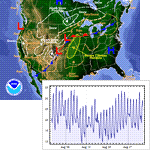
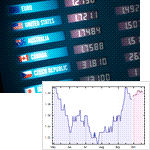
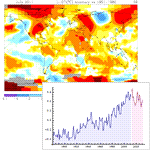
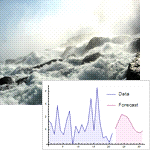
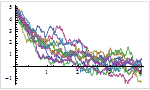
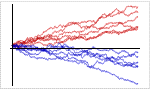
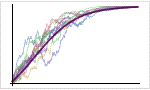
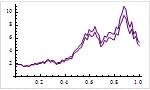
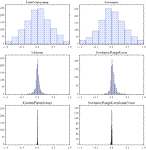
Mathematica 9には時系列と確率微分方程式によるランダム過程に対する広範なサポートが加わっている．定常成分・サポートする多項式成分と季節成分の両方に対応する，スカラーとベクトルによる時系列モデル一式が備わっている．時系列モデルは簡単にシミュレーションを行い，データから推定し，予測を生成するのに使うことができる．確率微分方程式過程は，パラメトリック過程と完全に汎用な伊藤過程・ストラトノビッチ(Stratonovich)過程のどれを使っても指定できる．確率微分方程式過程は数値的なシミュレーションが簡単に行え，記号的に計算することのできる特性も多数ある．
- スカラーとベクトルによる移動平均(MA)，自己回帰(AR)，自己回帰移動平均(ARMA)過程のサポート
- 長期記憶時系列の他，多項式および季節的トレンドを含む過程をサポート
- 時系列モデルからのシミュレーション，推定，予測に対する完全なサポート
- 偏相関関数およびスペクトル密度に対する追加の時系列サポート
- 拡張Dickey-Fuller検定やPhillips-Perron検定を含む，単位根に対する柔軟な検定
- Cox-Ingersoll-Ross等のパラメトリック確率微分方程式のサポート
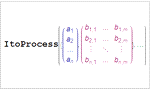
- 微分方程式によって定義されたスカラーおよびベクトルの伊藤過程とストラトノビッチ過程
- パラメトリック確率微分方程式過程を伊藤形式あるいはストラトノビッチ形式に自動変換
- 他の確率微分方程式過程によって動く伊藤およびストラトノビッチの確率微分方程式過程
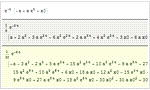
- 通常形式への自動変換を含む伊藤過程およびストラトノビッチ過程の非線形関数のサポート
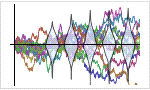
- オイラー・丸山法，確率ルンゲクッタ法等を含む確率微分方程式過程のシミュレーションに対する広範なサポート
- 平均値関数，時系列に対する分散関数，確率微分方程式過程の記号計算のサポート
関連関数RandomFunction 
ARMAProcess ARIMAProcess SARIMAProcess ARProcess MAProcess PowerSpectralDensity WeakStationarity ProcessParameterAssumptions TimeSeriesInvertibility TemporalData EstimatedProcess PartialCorrelationFunction KalmanFilter UnitRootTest SARMAProcess ProcessEstimator CorrelationFunction TimeSeriesForecast FindProcessParameters FARIMAProcess ItoProcess WienerProcess GeometricBrownianMotionProcess OrnsteinUhlenbeckProcess CoxIngersollRossProcess BrownianBridgeProcess StratonovichProcess SliceDistribution StationaryDistribution CovarianceFunction AbsoluteCorrelationFunction AdjustTimeSeriesForecast
ARMAProcess ARIMAProcess SARIMAProcess ARProcess MAProcess PowerSpectralDensity WeakStationarity ProcessParameterAssumptions TimeSeriesInvertibility TemporalData EstimatedProcess PartialCorrelationFunction KalmanFilter UnitRootTest SARMAProcess ProcessEstimator CorrelationFunction TimeSeriesForecast FindProcessParameters FARIMAProcess ItoProcess WienerProcess GeometricBrownianMotionProcess OrnsteinUhlenbeckProcess CoxIngersollRossProcess BrownianBridgeProcess StratonovichProcess SliceDistribution StationaryDistribution CovarianceFunction AbsoluteCorrelationFunction AdjustTimeSeriesForecast
