ラプラス演算子の固有値と固有関数

一次元領域上で，ラプラス演算子，つまり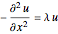 の解の固有値と固有関数を小さい方から4個求める．

ラプラス演算子を指定する．

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}];

固有値と固有関数を小さい方から4個数値的に求める．

In[2]:=

NDEigensystem[\[ScriptCapitalL], u[x], {x, 0, \[Pi]}, 4]

Out[2]=

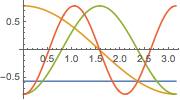
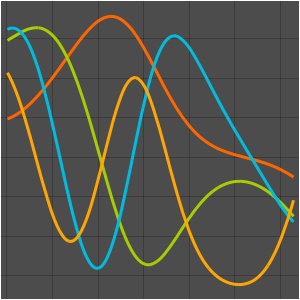
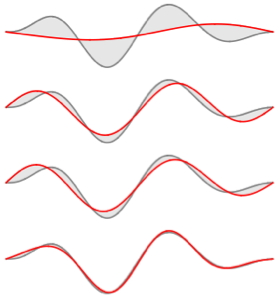
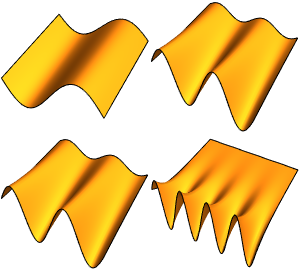
固有関数を可視化する．

In[3]:=

NDEigensystem[\[ScriptCapitalL], u[x], {x, 0, \[Pi]}, 4]; Plot[Evaluate[%[[2]]], {x, 0, \[Pi]}]

Out[3]=