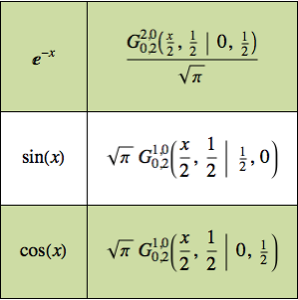Modele uma corrente pendurada
Encontre a posição com energia pontecial mínima de uma corrente ou cabo de comprimento 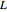 suspenso entre dois pontos.
suspenso entre dois pontos.
Defina os valores de parâmetro para o comprimento da correia 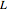 , a altura do lado esquerdo
, a altura do lado esquerdo 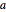 , e a altura do lado direito
, e a altura do lado direito 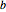 .
.
L = 4; a = 1; b = 3; Deixe que 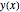 seja a altura da corrente como uma função de posição horizontal, com
seja a altura da corrente como uma função de posição horizontal, com 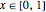 .
.
xf = 1; nh = 201; h := xf/nh;Defina as variáveis para a altura da corrente 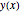 .
.
varsy = Array[y, nh + 1, {0, nh}];Determine a inclinação na posição 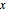 por
por 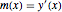 e as variáveis para a mesma.
e as variáveis para a mesma.
varsm = Array[m, nh + 1, {0, nh}];Determine a energia potencial parcial 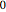 por
por 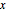 por
por  .
.
varsv = Array[v, nh + 1, {0, nh}];Determine o comprimento da corrente em posição 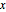 por
por 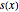 e determine as variáveis para a mesma.
e determine as variáveis para a mesma.
varss = Array[s, nh + 1, {0, nh}];Junte todas as variáveis.
vars = Join[varsm, varsy, varsv, varss];O objetivo é minimizar a energia potencial total 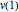 .
.
objfn = v[nh];Aqui estão as restrições de valores de limite da geometria.
bndcons = {y[0] == a, y[nh] == b, v[0] == 0, s[0] == 0, s[nh] == L}; Discretize a equação diferencial ordinária: 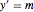 ,
, 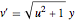 ,
, 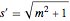 .
.
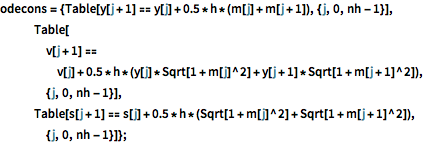
odecons = {Table[
y[j + 1] == y[j] + 0.5*h*(m[j] + m[j + 1]), {j, 0, nh - 1}],
Table[v[j + 1] ==
v[j] + 0.5*
h*(y[j]*Sqrt[1 + m[j]^2] + y[j + 1]*Sqrt[1 + m[j + 1]^2]), {j,
0, nh - 1}],
Table[s[j + 1] ==
s[j] + 0.5*h*(Sqrt[1 + m[j]^2] + Sqrt[1 + m[j + 1]^2]), {j, 0,
nh - 1}]};Escolha pontos iniciais para as variáveis.

tmin = If[b > a, 0.25 , 0.75]; init =
Join[Table[4*Abs[b - a]*((k/nh) - tmin), {k, 0, nh}],
Table[4*Abs[b - a]*(k/nh)*(0.5*(k/nh) - tmin) + a, {k, 0, nh}],
Table[(4*Abs[b - a]*(k/nh)*(0.5*(k/nh) - tmin) + a)*4*
Abs[b - a]*((k/nh) - tmin), {k, 0, nh}],
Table[4*Abs[b - a]*((k/nh) - tmin), {k, 0, nh}]];Minimize a energia potencial total, sujeita às restrições.
sol = FindMinimum[{objfn, Join[bndcons, odecons]},
Thread[{vars, init}]];Extraia os pontos de solução.
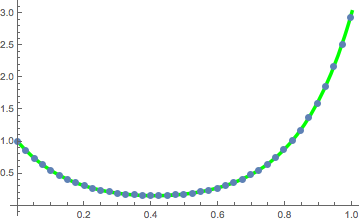
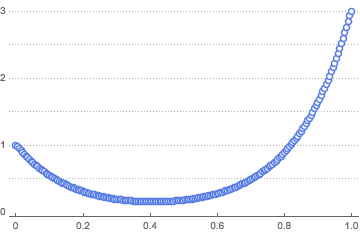
solpts = Table[{i h, y[i] /. sol[[2]]}, {i, 0, nh}];Faça uma representação gráfica da corrente com energia potencial mínima.
ListPlot[solpts, ImageSize -> Medium, PlotTheme -> "Marketing"]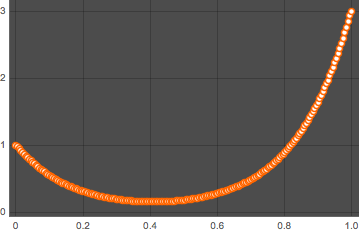
Use FindFit para ajustar o resultado à curva catenária.
catenary[t_] = c1 + (1/c2) Cosh[c2 (t - c3)];fitsol = FindFit[solpts, catenary[t], {c1, c2, c3}, {t}]Faça um gráfico da solução junto com a curva catenária.

Show[Plot[catenary[t] /. fitsol, {t, 0, 1},
PlotStyle -> Directive[Green, Thickness[0.01]],
ImageSize -> Medium],
ListPlot[Take[solpts, 1 ;; nh ;; 5], PlotStyle -> PointSize[.02]]]