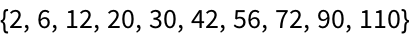| 38 | Assigning Names to Things |
Particularly when you’re doing quick experiments in the Wolfram Language, it’s often convenient to use % to refer to the result of your most recent computation.
Do a simple computation:
| In[1]:= |
| Out[1]= |
% gives the result of the previous computation:
| In[2]:= |
| Out[2]= |
This squares the most recent result:
| In[3]:= |
| Out[3]= |
If you expect to refer to a result later, you can assign it a name. For example, you can say thing=Range[10] to assign thing as a name for the result of Range[10].
Assign thing to be the result of Range[10]:
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= |
Square the value of thing:
| In[6]:= |
| Out[6]= |
You can assign a name to the result of a computation even if you never display the result. End your input with ; (semicolon) to avoid seeing the result.
Assign a name to a list of a million elements, but don’t display the list:
| In[7]:= |
| In[8]:= |
| Out[8]= |
When you assign a name to something, the name will stay until you explicitly clear it.
Assign x the value 42:
| In[9]:= |
| Out[9]= |
You might have thought this would be {x, y, z}—but x has value 42:
| In[10]:= |
| Out[10]= |
If you want to clear assignments, use Clear.
Clear any assignment for x:
| In[11]:= |
Now x, like y and z, isn’t replaced:
| In[12]:= |
| Out[12]= |
Assigning a global value for x, like x=42, is potentially a big deal, because it can affect everything you do in your session (at least until you clear x). Something that’s much safer—and extremely useful—is just to assign a temporary, local value to x, inside a module.
| In[13]:= |
| Out[13]= |
Outside the module, x still has no value assigned:
| In[14]:= |
| Out[14]= |
Define local variables x and n, then compute x^n using the values you’ve assigned:
| In[15]:= |
| Out[15]= |
In the functional style of programming that we’ve used in most of this book, you carry out sequences of operations by applying sequences of functions. This is a very powerful and direct style of programming that’s uniquely suited to the Wolfram Language.
But once one’s defining variables, one can use a different style, in which one doesn’t feed results directly from one function to another, but instead assigns them as values of variables to be used later. This kind of procedural programming is what’s been used in lower-level languages since the very earliest days of computing.
It’s still useful in the Wolfram Language, though in many ways it’s eclipsed by functional programming, as well as by the pattern-based style of programming that we’ll discuss later.
To specify sequences of actions in the Wolfram Language one just separates them by semicolons (;). (Putting a semicolon at the end is like specifying an empty final action, which is why this has the effect of not displaying a result.)
Do a sequence of operations; the result is what the last operation produces:
| In[16]:= |
| Out[16]= |
This defined global values for x and y; don’t forget to clear them:
| In[17]:= |
You can use semicolons to do sequences of operations inside Module.
This does a sequence of operations, with x and y maintained as local variables:
| In[18]:= |
| Out[18]= |
You can mix local variables that do and don’t have initial values:
| In[19]:= |
| Out[19]= |
You can nest modules—which is useful if you’re building large programs where you want to isolate different parts of your code.
| % | the most recent computation result | |
| x=value | assign a value | |
| Clear[x] | clear a value | |
| Module[{x=value}, ...] | set up a temporary variable | |
| expr; | do a computation, but don’t display its result | |
| expr1; expr2; ... | do a sequence of computations |
38.2Use Module to generate a list of 10 random integers up to 100, then make a column giving the original list, and the results of applying Sort, Max and Total to it. »
38.3Use Module to generate an image collage from a picture of a giraffe, and the results of applying Blur, EdgeDetect and ColorNegate to it. »
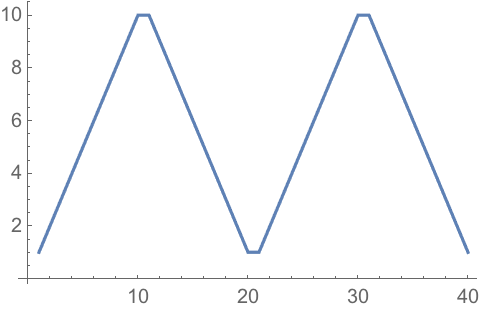
38.4Inside a Module, let r=Range[10], then make a line plot of r joined with the reverse of r joined with r joined with the reverse of r. »
38.7Generate 10 random strings made of 5 letters, in which consonants (non-vowels) alternate with vowels (aeiou). »
How come we’re at Section 38, and only now introducing variable assignments?
Because, as we’ve seen, in the Wolfram Language one can go a very long way without introducing them. And it tends to be a lot cleaner to program without them.
Can I assign a name to anything?
Yes. Graphics, arrays, images, pure functions, whatever.
How does one read x=4 out loud?
“x equals 4”, or, more rarely, “assign x to 4”, or “give x the value 4”.
Use names that are specific and explicit. Don’t worry if they’re long; they’ll get autocompleted when you type. For “informal” names, start with lowercase letters. For more carefully thought out names, consider using capitalization like built-in functions do.
% gives the previous result. What about the result before that, etc.?
%% gives the next to last, %%% gives the next-to-next-to-last, etc. %n gives the result on line n (i.e. the result labeled Out[n]).
Yes. x=y=6 assigns both x and y to 6. {x, y}={3, 4} assigns x to 3 and y to 4. {x, y}={y, x} swaps the values of x and y.
What happens if a variable escapes from a Module without having been assigned a value?
Try it! You’ll find you’ll get a new variable that’s been given a unique name.
The Wolfram Language has those. Do is sometimes worth using, particularly when your objective is side effects, like assigning variables or exporting data. For is almost always a bad idea, and can almost always be replaced by much cleaner code using constructs such as Table.
- The result of x=2+2 is just 4, but as a side effect an assignment is made for x.
- In pure functional programming, the only effect of any computation is to give the result. As soon as you’re assigning values, there’s effectively a hidden state that’s set up by those assignments.
- x=. is an alternative to Clear[x].
- Module does lexical scoping, which means it effectively localizes the names of variables. Block does dynamic scoping, which means it localizes the values, but not the names, of variables. Both are useful in different circumstances. Table effectively uses Block.
- x++ is equivalent to x=x+1. x+=n is equivalent to x=x+n. AppendTo[x, n] is equivalent to x=Append[x, n] or x=Join[x, {n}].