WOLFRAM

Explore the latest version of An Elementary Introduction to the Wolfram Language »
Stephen Wolfram
An Elementary Introduction to the Wolfram Language
Second Edition (2017)
45Datasets
Especially in larger organizations, computing often centers around dealing with large amounts of structured data. The Wolfram Language has a very powerful way to deal with structured data, using what it calls datasets.
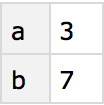
A simple example of a dataset is formed from an association of associations.
Create a simple dataset that can be viewed as having 2 rows and 3 columns:
In[1]:=
Click for copyable input
Out[1]=
The Wolfram Language displays most datasets in tabular form. You can extract parts from datasets just like you would from associations.
Get the element from “row b” and “column z”:
In[2]:=
Click for copyable input
Out[2]=
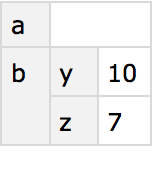
You can first extract the whole “b row”, then get the “z” element of the result:
In[3]:=
Click for copyable input
Out[3]=
You can also just get the whole “b row” of the dataset. The result is a new dataset, which for ease of reading happens to be displayed in this case as a column.
Generate a new dataset from the “b row” of the original dataset:
In[4]:=
Click for copyable input
Out[4]=
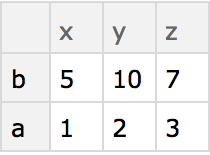
Here is the dataset that corresponds to the “z column” for all “rows”.
Generate a dataset consisting of the “z column” for all rows:
In[5]:=
Click for copyable input
Out[5]=
Extracting parts of datasets is just the beginning. Anywhere you can ask for a part you can also give a function that will be applied to all parts at that level.
Get totals for each row by applying Total to all columns for all the rows:
In[6]:=
Click for copyable input
Out[6]=
If we use f instead of Total, we can see what’s going on: the function is being applied to each of the “row” associations.
Apply the function f to each row:
In[7]:=
Click for copyable input
Out[7]=
Apply a function that adds the x and z elements of each association:
In[8]:=
Click for copyable input
Out[8]=
You can use any function; here’s PieChart:
In[9]:=
Click for copyable input
Out[9]=
You can give a function to apply to all rows too.
This extracts the value of each “z column”, then applies f to the association of results:
In[10]:=
Click for copyable input
Out[10]=
Apply f to the totals of all columns:
In[11]:=
Click for copyable input
Out[11]=
Find the maximum of these totals:
In[12]:=
Click for copyable input
Out[12]=
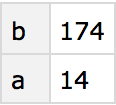
You can always “chain” queries, for example first finding the totals for all rows, then picking out the result for the “b row”.
Find totals for all rows, then pick out the total for the “b row”:
In[13]:=
Click for copyable input
Out[13]=
It’s equivalent to this:
In[14]:=
Click for copyable input
Out[14]=
Particularly when one’s dealing with large datasets, it’s common to want to select parts based on a criterion. The operator form of Select provides a very convenient way to do this.
Select numbers greater than 5 from a list:
In[15]:=
Click for copyable input
Out[15]=
Another way to get the same answer, using the operator form of Select:
In[16]:=
Click for copyable input
Out[16]=
The operator form of Select is a function which can be applied to actually perform the Select operation.
Make a dataset by selecting only rows whose “z column” is greater than 5:
In[17]:=
Click for copyable input
Out[17]=
For each row, select columns whose values are greater than 5, leaving a ragged structure:
In[18]:=
Click for copyable input
Out[18]=
Normal turns the dataset into an ordinary association of associations:
In[19]:=
Click for copyable input
Out[19]=
Many Wolfram Language functions have operator forms.
Sort according to the values of a function applied to each element:
In[20]:=
Click for copyable input
Out[20]=
SortBy has an operator form:
In[21]:=
Click for copyable input
Out[21]=
Sort rows according to the value of the difference of the x and y columns:
In[22]:=
Click for copyable input
Out[22]=
Sort the rows, and find the total of all columns:
In[23]:=
Click for copyable input
Out[23]=
Sometimes you want to apply a function to each element in the dataset.
Apply f to each element in the dataset:
In[24]:=
Click for copyable input
Out[24]=
Sort the rows before totaling the squares of their elements:
In[25]:=
Click for copyable input
Out[25]=
Datasets can contain arbitrary mixtures of lists and associations. Here’s a dataset that can be thought of as a list of records with named fields.
A dataset formed from a list of associations:
In[26]:=
Click for copyable input
Out[26]=
It’s OK for entries to be missing:
In[27]:=
Click for copyable input
Out[27]=
Now that we’ve seen some simple examples, it’s time to look at something slightly more realistic. Let’s import a dataset giving properties of planets and moons. The dataset has a hierarchical structure, with each planet having a mass and radius of its own, and then also having a collection of moons, each of which have their own properties. This general structure is extremely common in practice (think students and grades, customers and orders, etc.).
Get a hierarchical dataset of planets and moons from the cloud:
In[28]:=
Click for copyable input
Out[28]=
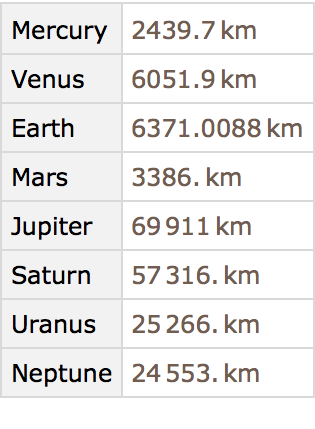
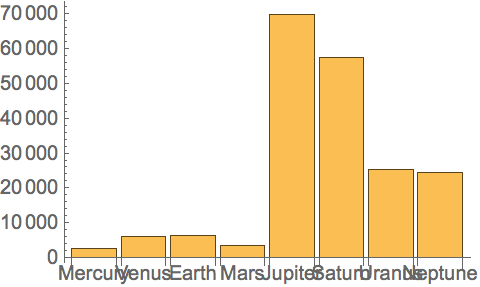
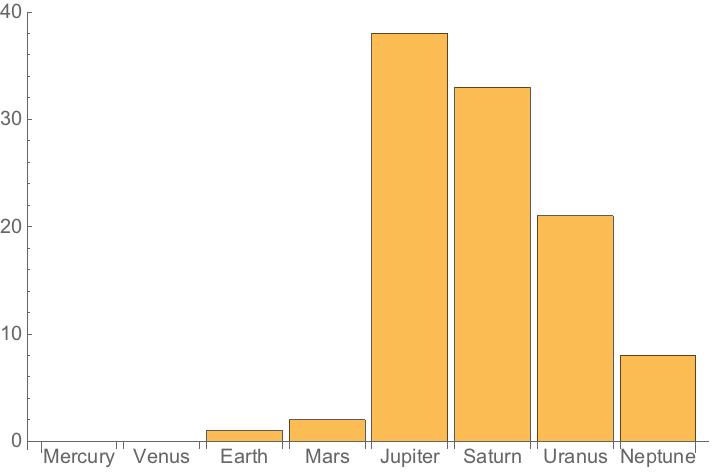
Find the radii of all the planets:
In[29]:=
Click for copyable input
Out[29]=
Make a bar chart of planet radii:
In[30]:=
Click for copyable input
Out[30]=
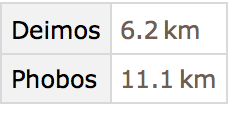
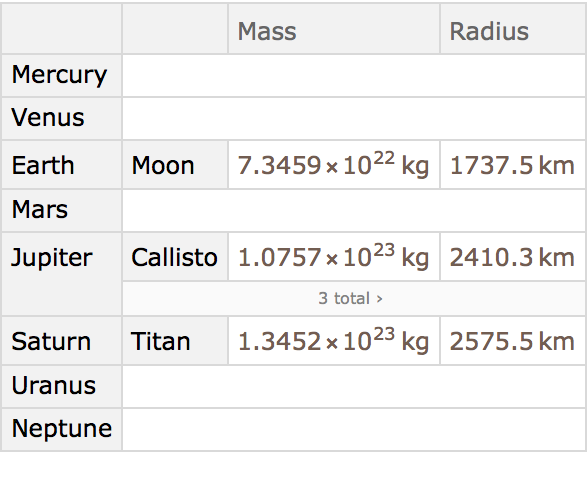
If we ask about the moons of Mars, we get a dataset, which we can then query further.
Get a dataset about the moons of Mars:
In[31]:=
Click for copyable input
Out[31]=
“Drill down” to make a table of radii of all the moons of Mars:
In[32]:=
Click for copyable input
Out[32]=
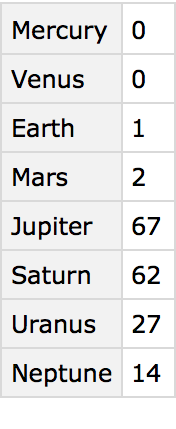
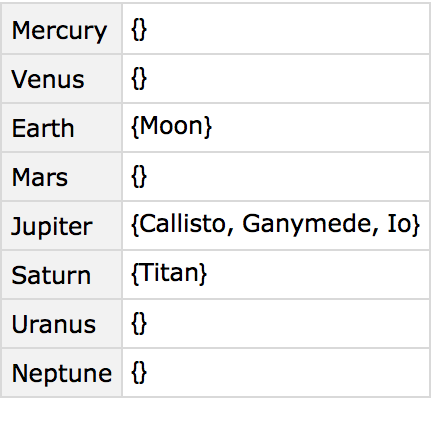
We can do computations about the moons of all planets. First, let’s just find out how many moons are listed for each planet.
Make a dataset of the number of moons listed for each planet:
In[33]:=
Click for copyable input
Out[33]=
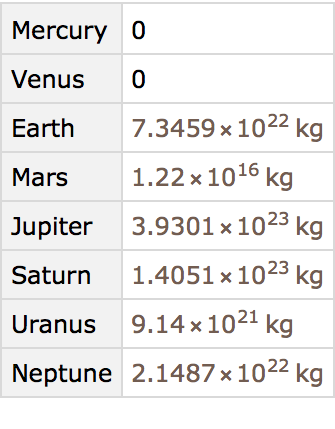
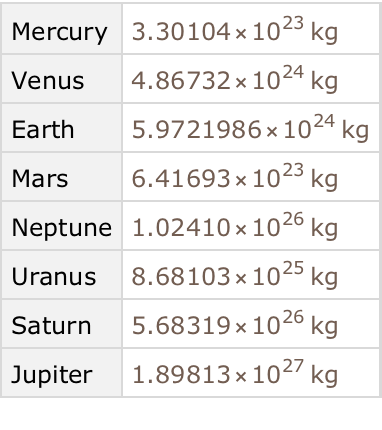
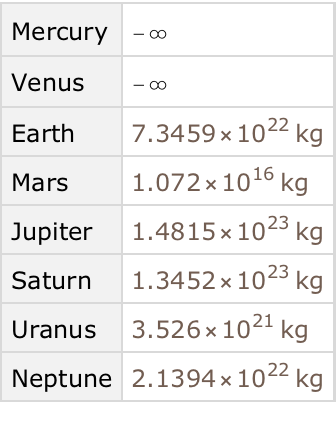
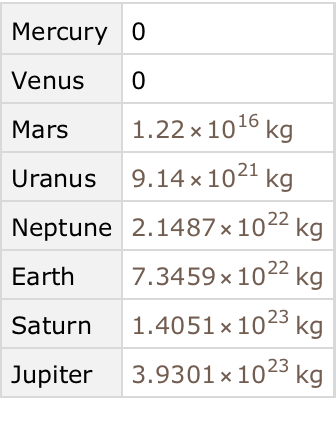
Find the total mass of all moons for each planet:
In[34]:=
Click for copyable input
Out[34]=
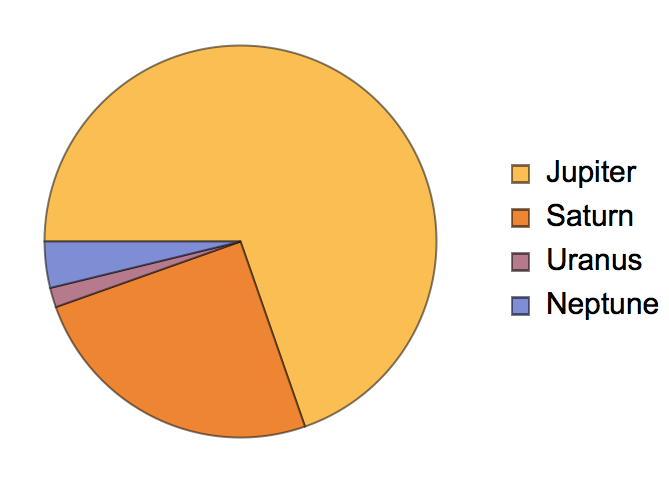
Get the same result, but only for planets with more than 10 moons:
In[35]:=
Click for copyable input
Out[35]=
Make a pie chart of the result:
In[36]:=
Click for copyable input
Out[36]=
Get a dataset with moons that are more than 1% of the mass of the Earth.
For all moons, select ones whose mass is greater than 0.01 times the mass of the Earth:
In[37]:=
Click for copyable input
Out[37]=
Get the list of keys (i.e. moon names) in the resulting association for each planet:
In[38]:=
Click for copyable input
Out[38]=
Get the underlying association:
In[39]:=
Click for copyable input
Out[39]=
Join together, or “catenate”, the lists for all keys:
In[40]:=
Click for copyable input
Out[40]=
Here’s the whole computation in one line:
In[41]:=
Click for copyable input
Out[41]=
Here’s one more example, where we find the logarithm of the mass of each moon, then make a number line plot of these values for each planet.
Make number line plots of the logarithms of masses for moons of each planet:
In[42]:=
Click for copyable input
Out[42]=
Here’s how to make a word cloud of names of moons, sized according to the masses of the moons. To do this, we need a single association that associates the name of each moon with its mass.
When given an association, WordCloud determines sizes from values in the association:
In[43]:=
Click for copyable input
Out[43]=
The function Association combines associations:
In[44]:=
Click for copyable input
Out[44]=
Generate the word cloud of moon masses:
In[45]:=
Click for copyable input
Out[45]=
For what it does, the code here is surprisingly simple. But we can make it slightly more streamlined by using @* or /*.
We’ve seen before that we can write something like f[g[x]] as f@g@x or x//g//f. We can also write it f[g[#]]&[x]. But what about f[g[#]]&? Is there a short way to write this? The answer is that there is, in terms of the function composition operators @* and /*.
f@*g@*h represents a composition of functions to be applied right-to-left:
In[46]:=
Click for copyable input
Out[46]=
h/*g/*f represents a composition of functions to be applied left-to-right:
In[47]:=
Click for copyable input
Out[47]=
Here’s the previous code rewritten using composition @*:
In[48]:=
Click for copyable input
Out[48]=
And using right composition /*:
In[49]:=
Click for copyable input
Out[49]=
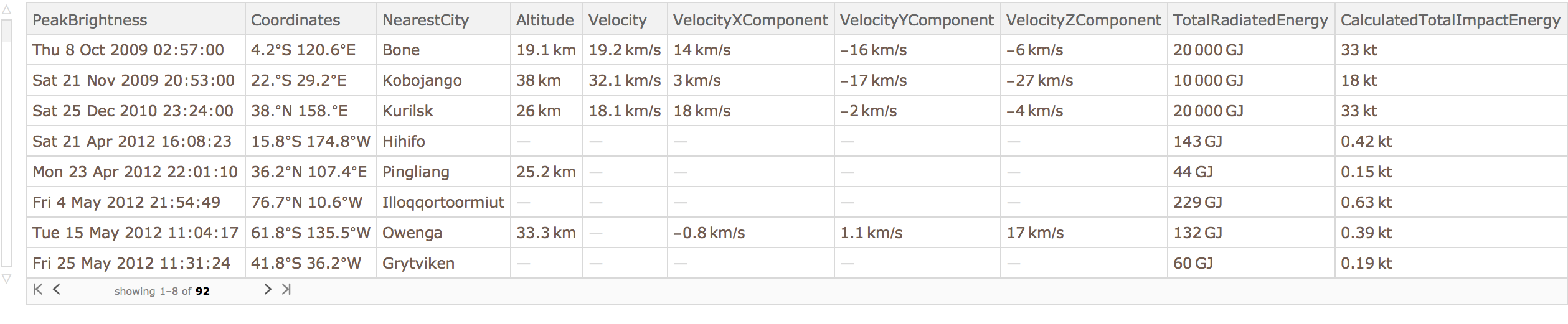
As a final example, let’s look at another dataset—this time coming straight from the Wolfram Data Repository. Here’s a webpage (about big meteors) from the repository:
To get the main dataset that’s mentioned here, just use ResourceData.
Get the dataset just by giving its name to ResourceData:
In[50]:=
Click for copyable input
Out[50]=
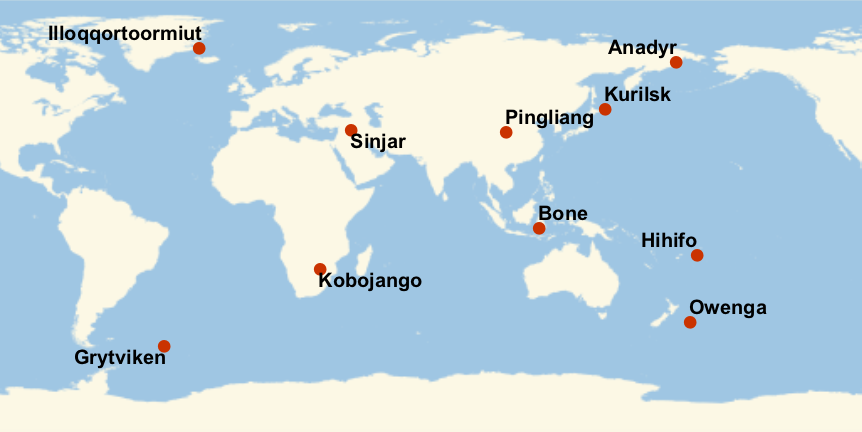
Extract the coordinates entry from each row, and plot the results:
In[51]:=
Click for copyable input
Out[51]=
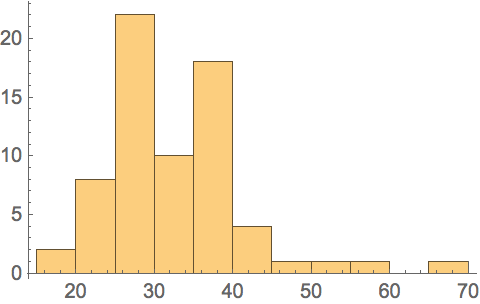
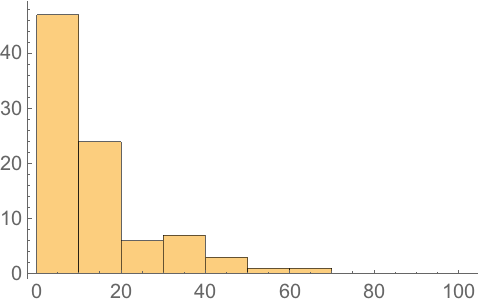
Make a histogram of the altitudes:
In[52]:=
Click for copyable input
Out[52]=
Vocabulary
Dataset[data] a dataset
Normal[dataset] convert a dataset to normal lists and associations
Catenate[{assoc1, ...}] catenate associations, combining their elements
f@*g composition of functions (f[g[x]] when applied to x)
f/*g right composition (g[f[x]] when applied to x)
Note: These exercises use the dataset planets=CloudGet["http://wolfr.am/7FxLgPm5"].
45.1Make a word cloud of the planets, with weights determined by their number of moons. »
Sample expected output:
Out[]=
45.2Make a bar chart of the number of moons for each planet. »
Sample expected output:
Out[]=
45.3Make a dataset of the masses of the planets, sorted by their number of moons. »
Sample expected output:
Out[]=
45.4Make a dataset of planets and the mass of each one’s most massive moon. »
Sample expected output:
Out[]=
45.5Make a dataset of masses of planets, where the planets are sorted by the largest mass of their moons. »
Sample expected output:
Out[]=
45.6Make a dataset of the median mass of all moons for each planet. »
Sample expected output:
Out[]=
Sample expected output:
Out[]=
45.8Make a word cloud of countries in Central America, with the names of countries proportional to the lengths of the Wikipedia article about them. »
Sample expected output:
Out[]=
45.9Find the maximum observed altitude in the Fireballs & Bolides dataset. »
Expected output:
Out[]=
45.10Find a dataset of the 5 largest observed altitudes in the Fireballs & Bolides dataset. »
Expected output:
Out[]=
45.11Make a histogram of the differences in successive peak brightness times in the Fireballs & Bolides dataset. »
Expected output:
Out[]=
45.12Plot the nearest cities for the first 10 entries in the Fireballs & Bolides dataset, labeling each city. »
Expected output:
Out[]=
45.13Plot the nearest cities for the 10 entries with largest altitudes in the Fireballs & Bolides dataset, labeling each city. »
Expected output:
Out[]=
Q&A
What kinds of data can datasets contain?
Any kinds. Not just numbers and text but also images, graphs and lots more. There’s no need for all elements of a particular row or column to be the same type.
Can I turn spreadsheets into datasets?
Yes. SemanticImport is often a good way to do it.
What are databases and how do they relate to Dataset?
Databases are a traditional way to store structured data in a computer system. Databases are often set up to allow both reading and writing of data. Dataset is a way to represent data that might be stored in a database so that it’s easy to manipulate with the Wolfram Language.
How does data in Dataset compare to data in an SQL (relational) database?
SQL databases are strictly based on tables of data arranged in rows and columns of particular types, with additional data linked in through “foreign keys”. Dataset can have any mixture of types of data, with any number of levels of nesting, and any hierarchical structure, somewhat more analogous to a NoSQL database, but with additional operations made possible by the symbolic nature of the language.
Can I use datasets to set up entities and values for them?
Yes. If you’ve got a dataset that’s an association of associations, with the outer keys being entities and the inner ones being properties, then you just have to put this inside EntityStore, and you’ll pretty much have everything set up.
Tech Notes
More to Explore
Guide to Computation with Structured Datasets in the Wolfram Language »
 
Download Notebook Version
es