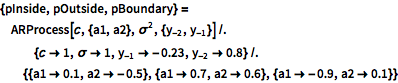Time Series Processes with Initial Conditions
Mathematica 10 supports time series processes with given past values, which cover both the stationary time series conditioned on past values as well as nonstationary time series with initial conditions. When autoregressive coefficients satisfy the stationarity condition, the process with initial values converges to the stationary process in the long run.
Define an autoregressive process with given past values.
| Out[1]= |  |
Find the mean function of the process.
| Out[2]= |  |
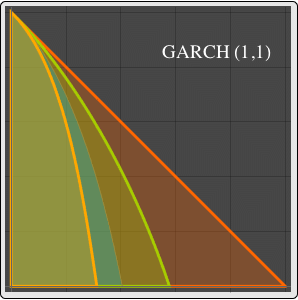
Form conditions for long‐run stability of the mean function.
| Out[3]= |  |
Verify that these conditions are equivalent to weak stationarity condition.
| Out[4]= |  |
| Out[5]= |  |
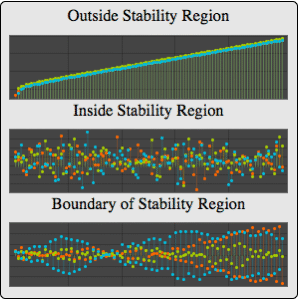
Visualize the parameter region and three sample parameter points—inside, outside, and on the boundary of the region of weak stationarity.
| Out[6]= |  |
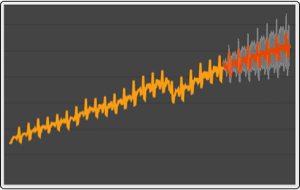
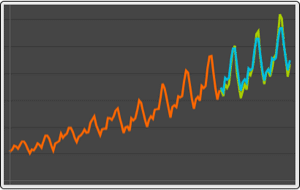
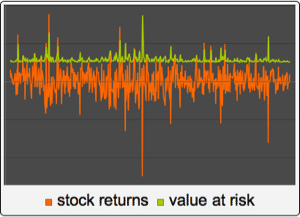
Visualize sample trajectories for a few parameter choices.
| Out[7]= |  |
| Out[8]= |  |
Visualize mean functions for these parameter choices.
| Out[9]= |  |