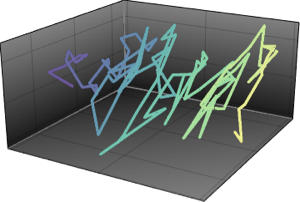
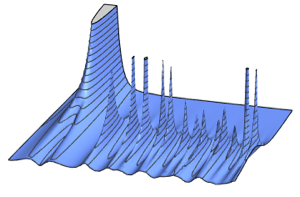
Brownian Motion on CUE

Brownian motion on the manifold of the unitary matrices can be constructed by infinitesimal generators from Gaussian unitary ensemble. The stationary distribution of this Brownian motion is then identical to the distribution of CUE.

In[1]:=

mats = RandomVariate[GaussianUnitaryMatrixDistribution[0.1, 2], 100000]; mats = Table[MatrixExp[I mat], {mat, mats}];

Generate a Brownian path with initial point sampled from CUE.

In[2]:=

initial = RandomVariate[CircularUnitaryMatrixDistribution[2]]; res = FoldList[#2.#1 &, initial, mats];

Compute the phases of the eigenvalues and compare them with the PDF of the eigenvalues of matrices from CUE.

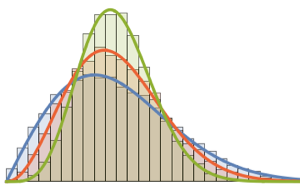
In[3]:=

phases = RandomSample /@ Arg[Eigenvalues /@ res];

In[4]:=

Show[ ContourPlot[ 1/(8 Pi^2) Abs[Exp[I \[Phi]1] - Exp[I \[Phi]2]]^2, {\[Phi]1, -Pi, Pi}, {\[Phi]2, -Pi, Pi}], ListPlot[Take[phases, {1, -1, 10}], ImageSize -> Medium, PlotStyle -> Black, PlotTheme -> "Detailed"], ImageSize -> Medium]

Out[4]=