Properties of Matrix Distributions

The lower-dimensional statistics derived from the random matrices play significant roles in characterizing the matrix ensembles. In various limiting situations, the distributions of these statistics collapse into different universality classes. MatrixPropertyDistribution provides a convenient access to sample and compute the numerical approximation of these derived properties.

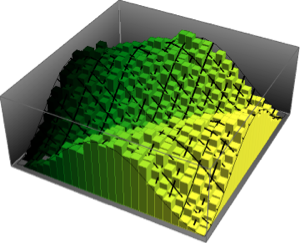
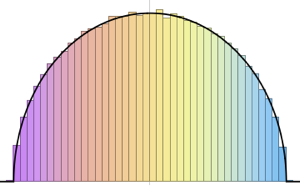
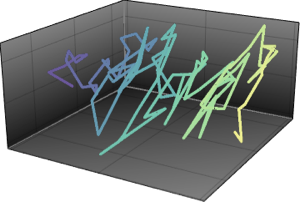
Sample the largest two eigenvalues from a Gaussian unitary ensemble.

In[1]:=

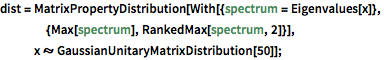
dist = MatrixPropertyDistribution[With[{spectrum = Eigenvalues[x]}, {Max[spectrum], RankedMax[spectrum, 2]}], x \[Distributed] GaussianUnitaryMatrixDistribution[50]];

In[2]:=

RandomVariate[dist]

Out[2]=

Visualize the joint distribution of the largest two eigenvalues based on the sampled result.

In[3]:=

sample = RandomVariate[dist, 10^4];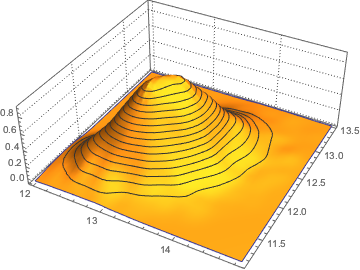

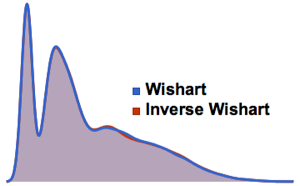
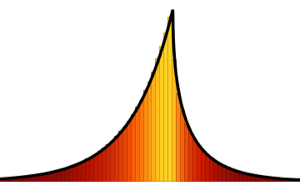
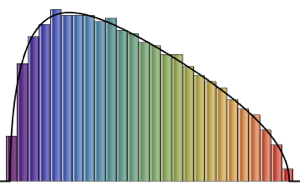
In[4]:=

SmoothHistogram3D[sample, "Scott", "PDF", PlotTheme -> "Detailed", ImageSize -> Medium]

Out[4]=

Sample the determinant of matrices from a Gaussian orthogonal ensemble and compare the empirical distribution with the closed-form expression.

In[5]:=

dist = MatrixPropertyDistribution[Det[x], x \[Distributed] GaussianOrthogonalMatrixDistribution[2]]; dets = RandomVariate[dist, 10^6];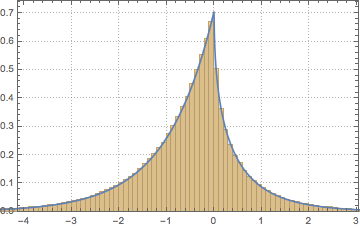

In[6]:=

empirical = Histogram[dets, {0.1}, PDF, PlotTheme -> "Detailed", ImageSize -> Medium]; detpdf[y_] := 1/Sqrt[2] Exp[ y] Piecewise[{{Erfc[Sqrt[2 y]], y >= 0}, {1, y < 0}}]; analytical = Plot[detpdf[y], {y, -5, 4}, Exclusions -> None, PlotLegends -> None, PlotTheme -> "Detailed", ImageSize -> Medium, Filling -> Axis]; Show[empirical, analytical]

Out[6]=

Approximate the mean of the determinant via Monte Carlo sampling and compare it with the actual value.

In[7]:=

{N@Mean[dist], Integrate[x detpdf[x], {x, -Infinity, Infinity}]}

Out[7]=