Dyson Coulomb Gas

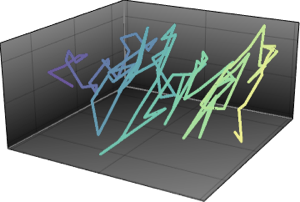
The joint distribution of the eigenvalues of a matrix following CircularOrthogonalMatrixDistribution is equivalent to the Boltzmann distribution of Dyson's Coulomb gas on a circle with inverse temperature 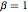. Define the average Hamiltonian (without the kinetic terms) per particle.

In[1]:=

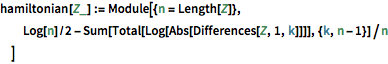
hamiltonian[Z_] := Module[{n = Length[Z]}, Log[n]/2 - Sum[Total[Log[Abs[Differences[Z, 1, k]]]], {k, n - 1}]/n ]

Define the distribution of the Hamiltonian.

In[2]:=

h\[ScriptCapitalD] = MatrixPropertyDistribution[hamiltonian[Eigenvalues[x]], x \[Distributed] CircularOrthogonalMatrixDistribution[n]];

Compute the sample mean of the Hamiltonian for systems of different size.

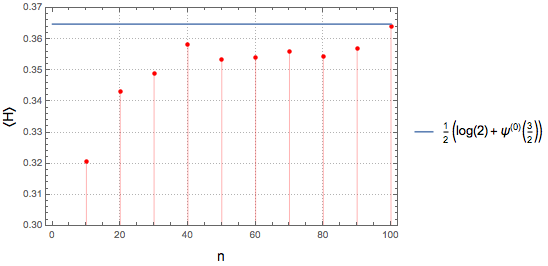
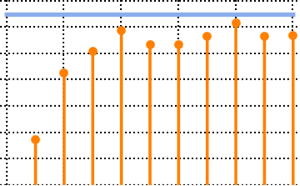
In[3]:=

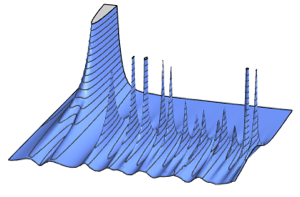
means = Table[{n, Mean[RandomVariate[h\[ScriptCapitalD], 1000]]}, {n, 10, 100, 10}];

Plot the sample means and compare them with the thermodynamic limit.

In[4]:=

Show[ListPlot[means, PlotStyle -> {Red, PointSize[Medium]}, Filling -> Axis, PlotRange -> {0.3, 0.37}, FrameLabel -> {Style["n", Black, 14], Style["\[LeftAngleBracket]H\[RightAngleBracket]", Black, 14]}, PlotTheme -> "Detailed"], Plot[1/2 (Log[2] + PolyGamma[0, 3/2]), {x, 0, 100}, PlotTheme -> "Detailed"]]

Out[4]=