Matrix Normal and Matrix T Distributions
Matrix normal and matrix 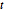 distributions are matrix variate normal and
distributions are matrix variate normal and 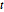 distributions with specified row and column scale matrices. Typical uses include time series analysis, random processes, and multivariate regression.
distributions with specified row and column scale matrices. Typical uses include time series analysis, random processes, and multivariate regression.
Given the scale matrices Σrow and Σcol, matrix normal distribution has probability density proportional to 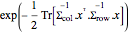 . Sample from a matrix normal distribution.
. Sample from a matrix normal distribution.
Subscript[\[CapitalSigma], row] = {{1, 0.9}, {0.9, 1}};
Subscript[\[CapitalSigma], col] = {{1, -0.9}, {-0.9, 1}};RandomVariate[
MatrixNormalDistribution[Subscript[\[CapitalSigma], row],
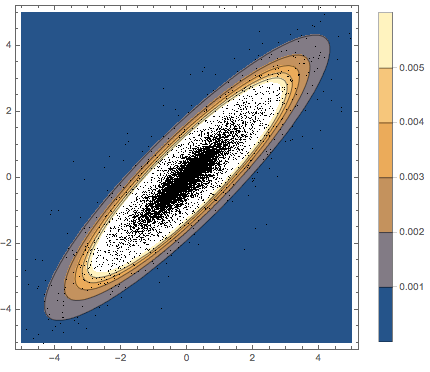
Subscript[\[CapitalSigma], col]]]Visualize the sampled row vectors on a scatter plot and compare it with the density function.
sample = RandomVariate[
MatrixNormalDistribution[Subscript[\[CapitalSigma], row],
Subscript[\[CapitalSigma], col]], 10^4];
firstrows = sample[[All, 1]];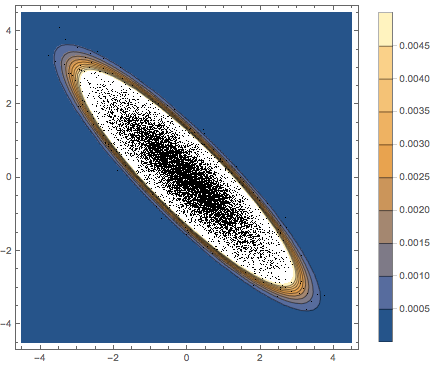
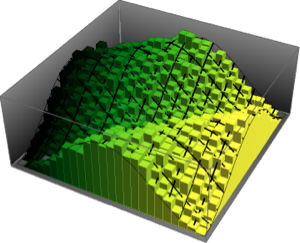
Visualize the sampled column vectors on a histogram and compare it with the density function.
firstcols = sample[[All, All, 1]];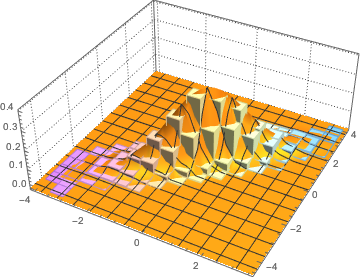
Similar to Student 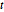 and multivariate
and multivariate 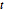 distributions, matrix
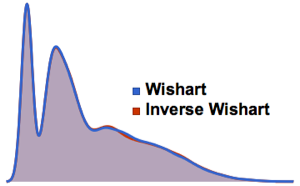
distributions, matrix  distribution is a mixture of matrix normal distribution with inverse Wishart distributed scale parameter. Sample from a matrix
distribution is a mixture of matrix normal distribution with inverse Wishart distributed scale parameter. Sample from a matrix 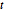 distribution.
distribution.
RandomVariate[
MatrixTDistribution[Subscript[\[CapitalSigma], row],
Subscript[\[CapitalSigma], col], 3]]Generate a set of matrix 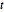 distributed matrices.
distributed matrices.
sample = RandomVariate[
MatrixTDistribution[Subscript[\[CapitalSigma], row],
Subscript[\[CapitalSigma], col], 3], 10^4];Lower-dimensional projections of matrix 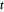 distributed variates are Student
distributed variates are Student 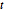 and multivariate
and multivariate  distributed. Project the sample to two-dimensional vectors and verify the goodness of fit.
distributed. Project the sample to two-dimensional vectors and verify the goodness of fit.
v = {1, 2};
vecs = sample.v;DistributionFitTest[vecs,
MultivariateTDistribution[
Subscript[\[CapitalSigma],
row] (v.Subscript[\[CapitalSigma], col].v)/3, 3]]Visualize the projected data on a scatter plot and compare it with the density function.