Marchenko–Pastur Distribution
Marchenko–Pastur distribution is the limiting distribution of eigenvalues of Wishart matrices as the matrix dimension 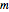 and degrees of freedom
and degrees of freedom  both tend to infinity with ratio
both tend to infinity with ratio 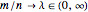 . For
. For 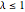 , the distribution has no point mass and the probability density function is well-defined.
, the distribution has no point mass and the probability density function is well-defined.
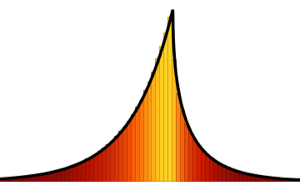
PDF[MarchenkoPasturDistribution[1/2], x]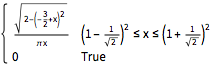
Sample from a Wishart distribution with identity scale matrix and compute the scaled eigenvalues.

n = 10^4;
m = 10^3;
eigs = RandomVariate[
MatrixPropertyDistribution[Eigenvalues[x]/n,
x \[Distributed]
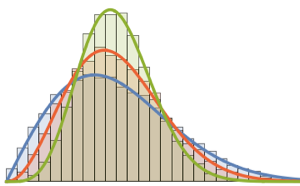
WishartMatrixDistribution[n, IdentityMatrix[m]]]];Compare the sampled result with the Marchenko–Pastur density function.

Show[Histogram[eigs, {0.05}, "PDF", ImageSize -> Medium,
PlotTheme -> "Detailed"],
Plot[PDF[MarchenkoPasturDistribution[m/n], x], {x, 0, 1.8},
PlotTheme -> "Detailed", PlotLegends -> None, Exclusions -> None]]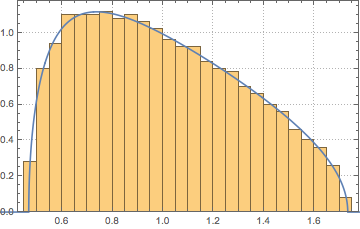
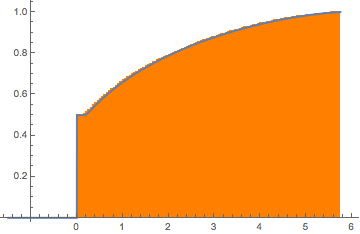
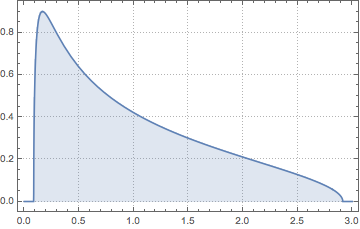
For 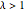 , the Wishart matrix is singular. With probability
, the Wishart matrix is singular. With probability 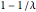 , the distribution has a point mass at
, the distribution has a point mass at 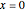 .
.
m = 500; n = 2 m;
CDF[MarchenkoPasturDistribution[n/m], 0]Generate a singular Wishart matrix with identity covariance and compute the scaled eigenvalues.
matrix = Transpose[#].# &[RandomVariate[NormalDistribution[], {m, n}]];
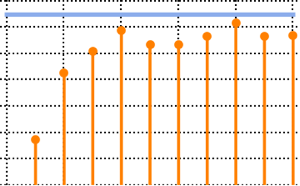
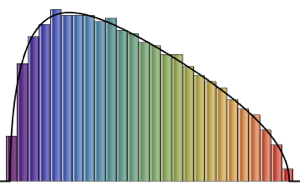
eigvs = Chop[Eigenvalues[matrix]/m];There is a gap in the density of eigenvalues near 0, and the bin at 0 has a large density.
Histogram[eigvs, {0.05}, PDF, PlotRange -> 1, ChartStyle -> Orange,
ImageSize -> Medium]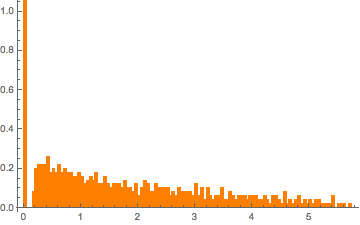
Fit MarchenkoPasturDistribution to the eigenvalues.
edist = EstimatedDistribution[eigvs,
MarchenkoPasturDistribution[\[Lambda], 1]]CDF of the fitted distribution shows a jump discontinuity at the origin.