Random Rotations

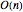CircularRealMatrixDistribution represents a uniform distribution of the orthogonal square matrices of dimension , also known as the Haar measure on the orthogonal group . The matrices generated according to this distribution can act as rotation operators for vectors in -dimensional vector space.

Define a distribution of random vectors obtained by rotating a fixed 3D vector (0,0,1) by a random matrix from CircularRealMatrixDistribution of dimension 3.

In[1]:=

\[ScriptCapitalD] = MatrixPropertyDistribution[r.{0, 0, 1}, r \[Distributed] CircularRealMatrixDistribution[3]];

Use this distribution to sample points on the surface of the unit sphere.

In[2]:=

points = RandomVariate[\[ScriptCapitalD], 10^3];

Check if all the sample points belong to the unit sphere.

In[3]:=

AllTrue[points, RegionMember[Sphere[3]]]

Out[3]=

Plot the sample points with the original vector.

In[4]:=

Graphics3D[{{Gray, PointSize[Small], Point[points]}, {Red, Thick, Arrow[{{0, 0, 0}, {0, 0, 1}}]}}, Axes -> True]

Out[4]=

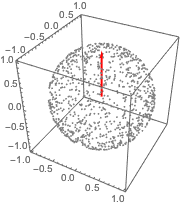
The element of surface area on the sphere in cylindrical coordinates is given by .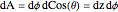

In[5]:=

{x, y, z} = Transpose[points]; \[Phi] = ArcTan[y/x];

Check if the marginal distributions of 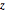and 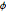are uniform.

In[6]:=

Histogram[#, 20, PDF] & /@ {\[Phi], z}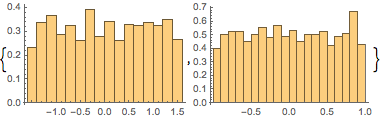

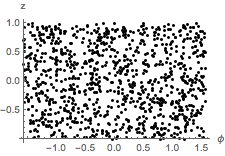
Out[6]=

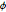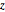Check if the sample points are uniformly distributed on the surface of the sphere by checking if the joint distribution of and is uniform.

In[7]:=

Graphics[Point[Transpose[{\[Phi], z}]], Axes -> True, AxesOrigin -> {-\[Pi]/2, -1}, AxesLabel -> {"\[Phi]", "z"}]

Out[7]=

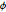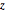Test the hypothesis that the joint distribution of and is uniform.

In[8]:=

DistributionFitTest[Transpose[{\[Phi], z}], UniformDistribution[{{-Pi/2, Pi/2}, {-1, 1}}], "TestConclusion"]

Out[8]=