Gaussian Ensembles (GOE, GUE, ...)

The Gaussian ensembles are families of normally distributed random matrices with distributions invariant under different unitary transformations. They are well studied, partly due to the analytical tractability, but also because the associated spectra closely approximate those of many systems with large degrees of freedom. Examples of these systems appear in physics, finance, and biology.

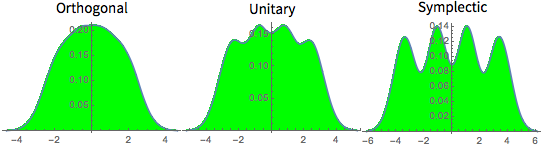
Matrices from the Gaussian orthogonal ensemble (GOE) are symmetric. »

In[1]:=

goe = RandomVariate[GaussianOrthogonalMatrixDistribution[5]];

In[2]:=

SymmetricMatrixQ[goe]

Out[2]=

Matrices from the Gaussian unitary ensemble (GUE) are Hermitian. »

In[3]:=

gue = RandomVariate[GaussianUnitaryMatrixDistribution[5]];

In[4]:=

HermitianMatrixQ[gue]

Out[4]=

Matrices from the Gaussian symplectic ensemble (GSE) are symplectic Hermitian. »

In[5]:=

symplecticMatrixQ[m_] := With[{\[ScriptCapitalJ] = KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[m]/2]]}, Conjugate[m].\[ScriptCapitalJ] == \[ScriptCapitalJ].m ];

In[6]:=

gse = RandomVariate[GaussianSymplecticMatrixDistribution[5]];

In[7]:=

symplecticMatrixQ[gse] && HermitianMatrixQ[gse]

Out[7]=

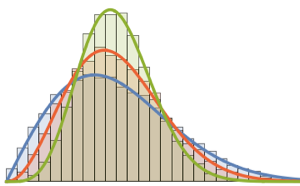
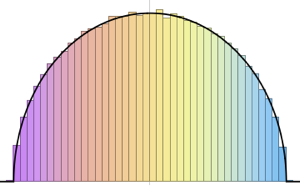
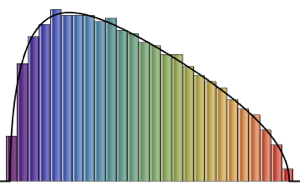
Distribution of eigenvalues for matrices from Gaussian ensembles at small dimensions.

In[8]:=

eigs = Flatten[ RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] #], 10^5]] & /@ {GaussianOrthogonalMatrixDistribution[4], GaussianUnitaryMatrixDistribution[4], GaussianSymplecticMatrixDistribution[4]}; Row[MapThread[ SmoothHistogram[#1, "Scott", Frame -> None, PlotLegends -> Placed[#2, Above], Filling -> Axis, FillingStyle -> Green] &, {eigs, {Style["Orthogonal", 15], Style["Unitary", 15], Style["Symplectic", 15]}}]]

Out[8]=