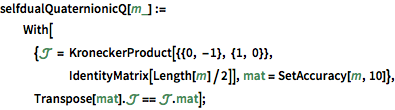Circular Ensembles (COE, CUE, ...)

The circular ensembles are families of unitary matrices with distributions invariant under different unitary transformations. Typical applications are in statistical mechanics, number theory, combinatorics, and nuclear physics.

Matrices from the circular real ensemble (CRE) are orthogonal. »

In[1]:=

cre = RandomVariate[CircularRealMatrixDistribution[5]];

In[2]:=

OrthogonalMatrixQ[cre]

Out[2]=

Matrices from the circular unitary ensemble (CUE) are unitary. »

In[3]:=

cue = RandomVariate[CircularUnitaryMatrixDistribution[5]];

In[4]:=

UnitaryMatrixQ[cue]

Out[4]=

Matrices from the circular orthogonal ensemble (COE) are symmetric and unitary. »

In[5]:=

coe = RandomVariate[CircularOrthogonalMatrixDistribution[5]];

In[6]:=

SymmetricMatrixQ[coe] && UnitaryMatrixQ[coe]

Out[6]=

Matrices from the circular symplectic ensemble (CSE) are self-dual unitary quaternionic. »

In[7]:=

selfdualQuaternionicQ[m_] := With[{\[ScriptCapitalJ] = KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[m]/2]], mat = SetAccuracy[m, 10]}, Transpose[mat].\[ScriptCapitalJ] == \[ScriptCapitalJ].mat];

In[8]:=

cse = RandomVariate[CircularSymplecticMatrixDistribution[5]];

In[9]:=

UnitaryMatrixQ[cse] && selfdualQuaternionicQ[cse]

Out[9]=

Matrices from the circular quaternion ensemble (CQE) are symplectic unitary. »

In[10]:=

symplecticMatrixQ[mat_] := With[{\[ScriptCapitalJ] = KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[mat]/2]] }, Conjugate[mat].\[ScriptCapitalJ] == \[ScriptCapitalJ].mat];

In[11]:=

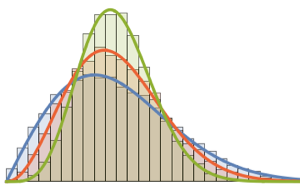
cqe = RandomVariate[CircularQuaternionMatrixDistribution[5]];

In[12]:=

UnitaryMatrixQ[cqe] && symplecticMatrixQ[cqe]

Out[12]=

Eigenvalues of matrices from CUE, COE, and CSE have unit length and are uniformly distributed in phase.

In[13]:=

args = Flatten[ Arg[RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] #], 10^4]]] & /@ {CircularUnitaryMatrixDistribution[5], CircularOrthogonalMatrixDistribution[5], CircularSymplecticMatrixDistribution[5]}; Row[MapThread[ Histogram[#1, {-Pi, Pi, Pi/10}, Frame -> None, ChartLegends -> Placed[#2, Above]] &, {args, {Style["Unitary", 15], Style["Orthogonal", 15], Style["Symplectic", 15]}}]]

Out[13]=

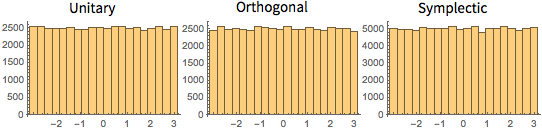
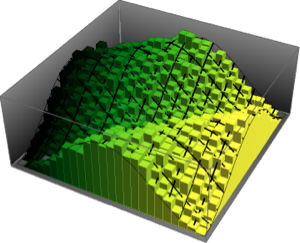
Visualize the joint distribution of the phase of the eigenvalues from two-dimensional CUE and compare it with the actual density.

In[14]:=

evs\[ScriptCapitalD] = MatrixPropertyDistribution[Arg[Eigenvalues[x]], x \[Distributed] CircularUnitaryMatrixDistribution[2]]; \[CurlyPhi]s = RandomSample /@ RandomVariate[evs\[ScriptCapitalD], 10^5];

In[14]:=

Show[ Histogram3D[\[CurlyPhi]s, {-Pi, Pi, 0.25}, PDF, PlotTheme -> "Scientific", ChartStyle -> "AvocadoColors"], Plot3D[1/(8 Pi^2) Abs[Exp[I \[Phi]1] - Exp[I \[Phi]2]]^2, {\[Phi]1, -Pi, Pi}, {\[Phi]2, -Pi, Pi}, PlotStyle -> None, MeshStyle -> Thick], ImageSize -> Medium]

Out[15]=