Wishart 和逆 Wishart 分布
Wishart 分布是从独立多维正态随机向量中所抽取样本的协方差矩阵的分布. 它是 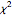 分布的多维推广. 该分布在诸如回归、协方差等多元统计中自然出现.
分布的多维推广. 该分布在诸如回归、协方差等多元统计中自然出现.
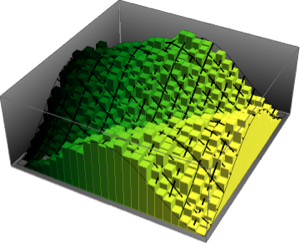
生成一个随机正定矩阵,用作 Wishart 分布的参数.
In[1]:=
\[CapitalSigma] = DiagonalMatrix[RandomReal[10, 5]];由 Wishart 分布得到的矩阵是对称正定矩阵. »
In[2]:=
dist = WishartMatrixDistribution[30, \[CapitalSigma]];
mat = RandomVariate[dist];In[3]:=
SymmetricMatrixQ[mat] && PositiveDefiniteMatrixQ[mat]Out[3]=
逆 Wishart 分布是由 Wishart 分布得到的逆矩阵的分布. »
In[4]:=
invdist =
InverseWishartMatrixDistribution[30, Inverse[\[CapitalSigma]]];
invmat = RandomVariate[invdist];由逆 Wishart 分布得到的矩阵是对称正定矩阵.
In[5]:=
SymmetricMatrixQ[invmat] && PositiveDefiniteMatrixQ[invmat]Out[5]=
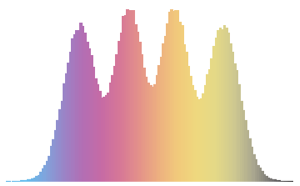
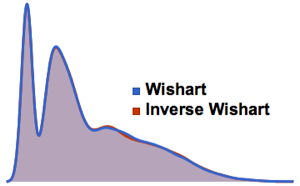
比较由 Wishart 和逆 Wishart 分布得到的矩阵的特征值分布.
In[6]:=

eigs = Flatten[
RandomVariate[
MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] dist],
10^4]];
inveigs =
Flatten[RandomVariate[
MatrixPropertyDistribution[Eigenvalues[x]^-1,
x \[Distributed] invdist], 10^4]];显示完整的 Wolfram 语言输入
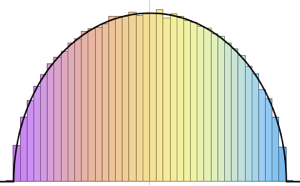
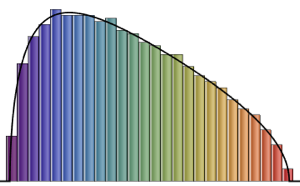
Out[7]=
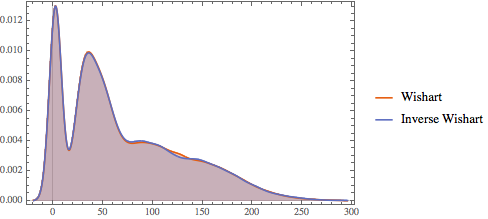
对于任何非零向量 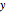 和尺度矩阵为
和尺度矩阵为 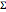 的 Wishart 矩阵
的 Wishart 矩阵 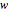 ,统计量
,统计量 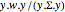 为
为 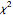 分布.
分布.
In[8]:=

y = #/Sqrt[#.\[CapitalSigma].#] &[RandomReal[1, 5]];
data = RandomVariate[
MatrixPropertyDistribution[y.w.y,
w \[Distributed] WishartMatrixDistribution[30, \[CapitalSigma]]],
10^4];In[9]:=
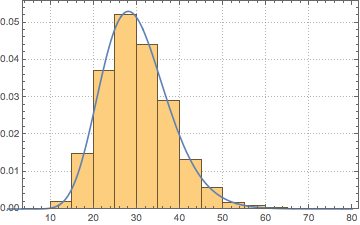
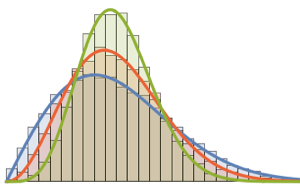
Show[Histogram[data, Automatic, PDF, PlotTheme -> "Detailed"],
Plot[PDF[ChiSquareDistribution[30], x], {x, 0, 80}],
ImageSize -> Medium]Out[9]=